Točno
21. listopada 2013. 16:06 (12 godine, 4 mjeseci)
Sakrij rješenje
Dokaži indukcijom da je suma prvih

kvadrata prirodnih brojeva jednaka
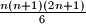
.
%V0
Dokaži indukcijom da je suma prvih $n$ kvadrata prirodnih brojeva jednaka $\frac{n(n+1)(2n+1)}{6}$.
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
Baza
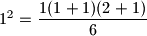
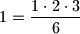
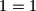
Ova tvrdnja ocito vrijedi
PretpostavkaPretpostavimo da vrijedi
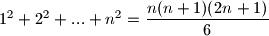
za neki prirodan broj
 Korak
KorakZelimo dokazati da
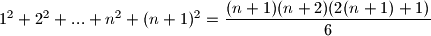
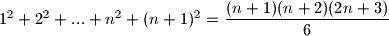
Iz pretpostavke znamo da je
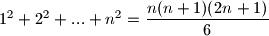
, pa uvrstimo to
Dobivamo:
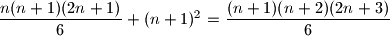
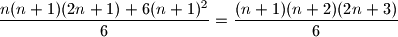
Djeljenjem cijele jednadzbe sa

i mnozenjem sa

dobivamo:
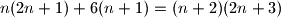
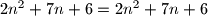
Sto ocito vrijedi
%V0
[b]Baza[/b]
$n=1$
$1^2=\dfrac{1(1+1)(2+1)}{6}$
$1=\dfrac{1\cdot 2 \cdot 3}{6}$
$1=1$
Ova tvrdnja ocito vrijedi
[b]Pretpostavka[/b]
Pretpostavimo da vrijedi
$1^2+2^2+...+n^2=\dfrac{n(n+1)(2n+1)}{6}$
za neki prirodan broj $n$
[b]Korak[/b]
Zelimo dokazati da
$1^2+2^2+...+n^2+(n+1)^2=\dfrac{(n+1)(n+2)(2(n+1)+1)}{6}$
$1^2+2^2+...+n^2+(n+1)^2=\dfrac{(n+1)(n+2)(2n+3)}{6}$
Iz pretpostavke znamo da je
$1^2+2^2+...+n^2=\dfrac{n(n+1)(2n+1)}{6}$, pa uvrstimo to
Dobivamo:
$\dfrac{n(n+1)(2n+1)}{6}+(n+1)^2=\dfrac{(n+1)(n+2)(2n+3)}{6}$
$\dfrac{n(n+1)(2n+1)+6(n+1)^2}{6}=\dfrac{(n+1)(n+2)(2n+3)}{6}$
Djeljenjem cijele jednadzbe sa $n+1$ i mnozenjem sa $6$ dobivamo:
$n(2n+1) + 6(n+1)=(n+2)(2n+3)$
$2n^2 +7n+6=2n^2 + 7n +6$
Sto ocito vrijedi
| 21. listopada 2013. 19:29 | ikicic | Točno |