Točno
21. listopada 2013. 20:52 (12 godine, 4 mjeseci)
Sakrij rješenje
Sakrij rješenje
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
Kliknite ovdje kako biste prikazali rješenje.
Kako ovu tvrdnju trebamo dokazati za sve prirodne brojeve strogo vece od  , kao bazu uzimamo
, kao bazu uzimamo 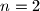 . (za
. (za 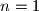 tvrdnja uopce ne vrijedi)
tvrdnja uopce ne vrijedi)
Baza

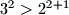
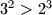
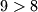
Ova tvrdnja ocito vrijedi
Pretpostavka
Pretpostavimo da vrijedi
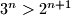
za neki prirodan broj
Korak
Zelimo dokazati da
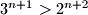
Da bi smo mogli iskoristiti pretpostavku, ovaj izraz moramo zapisati sto slicnije pretpostavci mozemo.
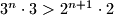
Iz pretpostavke znamo da je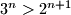 , a znamo i da je
, a znamo i da je 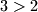 , pa je jasno da ce umnozak dva veca broja biti veci od umnoska dva manja broja.
, pa je jasno da ce umnozak dva veca broja biti veci od umnoska dva manja broja.
 , kao bazu uzimamo
, kao bazu uzimamo 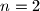 . (za
. (za 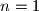 tvrdnja uopce ne vrijedi)
tvrdnja uopce ne vrijedi)Baza

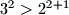
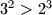
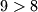
Ova tvrdnja ocito vrijedi
Pretpostavka
Pretpostavimo da vrijedi
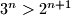
za neki prirodan broj

Korak
Zelimo dokazati da
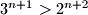
Da bi smo mogli iskoristiti pretpostavku, ovaj izraz moramo zapisati sto slicnije pretpostavci mozemo.
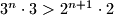
Iz pretpostavke znamo da je
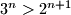 , a znamo i da je
, a znamo i da je 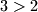 , pa je jasno da ce umnozak dva veca broja biti veci od umnoska dva manja broja.
, pa je jasno da ce umnozak dva veca broja biti veci od umnoska dva manja broja.  Školjka
Školjka 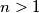 .
.