Školjka

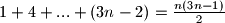
%V0 [b]Baza[/b] $n=1$ $1=\dfrac{1\cdot(3\cdot1 - 1)}{2}$ $1=1$ [b]Pretpostavka[/b] $1 + 4 + ... + (3n-2)=\dfrac{n(3n-1)}{2}$ Za neki prirodni broj $n$ [b]Korak[/b] Zelimo dokazati $1 + 4 + ... + (3n-2) + (3(n+1)-2)=\dfrac{(n+1)(3(n+1)-2)}{2}$ $1+4+...+(3n-2)+(3n+1)=\dfrac{(n+1)(3n+2)}{2}$ Iz pretpostavke znamo da je $1 + 4 + ... + (3n-2)=\dfrac{n(3n-1)}{2}$ pa uvrstavanjem dobivamo: $\dfrac{n(3n-1)}{2} + (3n+1)=\dfrac{(n+1)(3n+2)}{2}$ $n(3n-1)+2(3n+1)=(n+1)(3n+2)$ $3n^2 - n + 6n + 2 = (n+1)(3n+2)$ $3n^2 +5n +2 = (n+1)(3n+2)$ $(n+1)(3n+2)=(n+1)(3n+2)$