Točno
21. listopada 2013. 20:53 (12 godine, 4 mjeseci)
Sakrij rješenje
Zadan je niz

kao
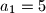
,
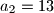
i
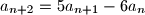
za

. Dokaži da za svaki član tog niza vrijedi
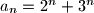
.
(

označava

-ti član niza. Ovdje su članovi niza definirani preko dva prethodna, tako je
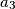
definiran kao

, a
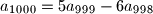
. Budući da jednakost vrijedi za svaki prirodni broj

, broj

je definiran za svaki prirodni broj

.)
%V0
Zadan je niz $a_n$ kao $a_1 = 5$, $a_2=13$ i $a_{n+2}=5a_{n+1}-6a_n$ za $n \in \mathbb{N}$. Dokaži da za svaki član tog niza vrijedi $a_n=2^n + 3^n$.
($a_n$ označava $n$-ti član niza. Ovdje su članovi niza definirani preko dva prethodna, tako je $a_3$ definiran kao $5a_2- 6a_1$, a $a_{1000}=5a_{999}-6a_{998}$. Budući da jednakost vrijedi za svaki prirodni broj $n$, broj $a_n$ je definiran za svaki prirodni broj $n$.)
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
%V0
Buduci da je svaki clan niza definiran preko dva prethodna clana vjerojatno bi bilo korisno imati pretpostavku i za $n-1$, a ne samo za $n$, no za tako nesto potrebno je imati dvije baze. (U ovom slucaju za $1$ i $2$)
[b]Baza[/b]
$n=1$
$a_1=2+3$
$5=5$
$n=2$
$a_2=2^2 + 3^2$
$13 = 9 +4$
$13=13$
[b]Pretpostavka[/b]
$a_{n-1}=2^{n-1}+3^{n-1}$
$a_n=2^n + 3^n$\
Za neki prirodni broj $n>1$
[b]Korak[/b]
Zelimo dokazati $a_{n+1}=2^{n+1}+3^{n+1}$
Po definiciji $a_{n+1}=5a_n -6a_{n-1}$
Uvrstavanjem pretpostavke dobivamo:
$a_{n+1}= 5(2^n+3^n)-6(2^{n-1}+3^{n-1})$
$a_{n+1}=5\cdot 2^n+5\cdot 3^n-6\cdot 2^{n-1}-6\cdot 3^{n-1}$
$a_{n+1}=10\cdot 2^{n-1} - 6\cdot 2^{n-1} + 15 \cdot 3^{n-1} - 6 \cdot 3^{n-1}$
$a_{n+1}=4\cdot 2^{n-1} + 9 \cdot 3^{n-1}$
$a_{n+1}=2^{n+1} + 3^{n+1}$
| 21. listopada 2013. 20:54 | ikicic | Točno |
 , a ne samo za
, a ne samo za  , no za tako nesto potrebno je imati dvije baze. (U ovom slucaju za
, no za tako nesto potrebno je imati dvije baze. (U ovom slucaju za  i
i  )
)
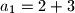
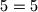

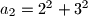
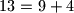
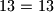
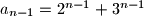
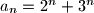
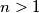
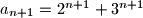
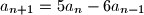
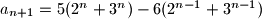
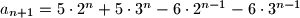
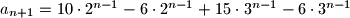
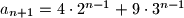
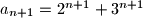
 , a ne samo za
, a ne samo za  , no za tako nesto potrebno je imati dvije baze. (U ovom slucaju za
, no za tako nesto potrebno je imati dvije baze. (U ovom slucaju za  i
i  )
)
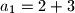
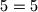

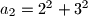
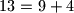
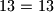
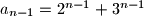
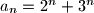
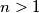
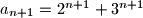
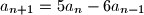
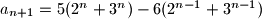
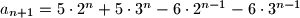
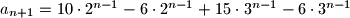
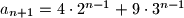
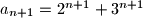
 Školjka
Školjka  kao
kao 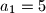 ,
, 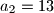 i
i 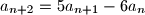 za
za  . Dokaži da za svaki član tog niza vrijedi
. Dokaži da za svaki član tog niza vrijedi 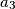 definiran kao
definiran kao  , a
, a 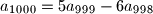 . Budući da jednakost vrijedi za svaki prirodni broj
. Budući da jednakost vrijedi za svaki prirodni broj