Točno
23. listopada 2013. 18:08 (12 godine, 4 mjeseci)
Sakrij rješenje
Sakrij rješenje
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
Kliknite ovdje kako biste prikazali rješenje.
Baza
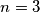
Trokut ima dijagonala, a
dijagonala, a 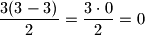
Dakle, baza je dokazana.
Pretpostavka
 -terokut ima tocno
-terokut ima tocno 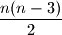 dijagonala.
dijagonala.
Korak
Zelimo dokazati da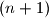 -terkokut ima
-terkokut ima 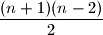 dijagonala.
dijagonala.
Oznacimo neka tri uzastopna vrha tog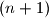 -terokuta sa
-terokuta sa  ,
,  , i
, i  , tako da je
, tako da je  izmedu
izmedu  i
i  . Sada povucimo duzinu
. Sada povucimo duzinu  .
.
Dobili smo -terokut (iz
-terokut (iz 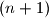 -terokuta smo izbacili jedan vrh, konkretno
-terokuta smo izbacili jedan vrh, konkretno  ) i trokut
) i trokut  . U
. U  -teroktu, po pretpostavci, ima
-teroktu, po pretpostavci, ima 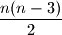 dijagonala. U trokutu ih ima
dijagonala. U trokutu ih ima  .
.
Sve dijagonale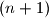 -terokuta koje jos nismo brojali zavrsavaju u tocki
-terokuta koje jos nismo brojali zavrsavaju u tocki  . Takvih dijagonala ima
. Takvih dijagonala ima 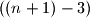 (
( mozemo povezati sa svim vrhovima osim sa njime samim, a sa svoja dva susjedna vrha daje stranice, a ne dijagonale). I jos nismo brojali duzinu
mozemo povezati sa svim vrhovima osim sa njime samim, a sa svoja dva susjedna vrha daje stranice, a ne dijagonale). I jos nismo brojali duzinu  , koja je u
, koja je u  -terokutu stranica, ali u
-terokutu stranica, ali u 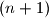 -terokutu je dijagonala.
-terokutu je dijagonala.
Dakle, ukupno imamo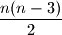 dijagonala iz
dijagonala iz  -terokuta,
-terokuta, 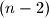 dijagonale iz tocke
dijagonale iz tocke  i dijagonalu
i dijagonalu  , sto je u sumi
, sto je u sumi
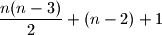
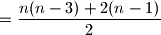
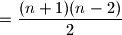
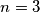
Trokut ima
 dijagonala, a
dijagonala, a 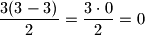
Dakle, baza je dokazana.
Pretpostavka
 -terokut ima tocno
-terokut ima tocno 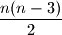 dijagonala.
dijagonala.Korak
Zelimo dokazati da
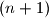 -terkokut ima
-terkokut ima 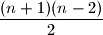 dijagonala.
dijagonala.Oznacimo neka tri uzastopna vrha tog
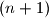 -terokuta sa
-terokuta sa  ,
,  , i
, i  , tako da je
, tako da je  izmedu
izmedu  i
i  . Sada povucimo duzinu
. Sada povucimo duzinu  .
.Dobili smo
 -terokut (iz
-terokut (iz 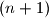 -terokuta smo izbacili jedan vrh, konkretno
-terokuta smo izbacili jedan vrh, konkretno  ) i trokut
) i trokut  . U
. U  -teroktu, po pretpostavci, ima
-teroktu, po pretpostavci, ima 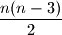 dijagonala. U trokutu ih ima
dijagonala. U trokutu ih ima  .
. Sve dijagonale
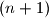 -terokuta koje jos nismo brojali zavrsavaju u tocki
-terokuta koje jos nismo brojali zavrsavaju u tocki  . Takvih dijagonala ima
. Takvih dijagonala ima 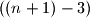 (
( mozemo povezati sa svim vrhovima osim sa njime samim, a sa svoja dva susjedna vrha daje stranice, a ne dijagonale). I jos nismo brojali duzinu
mozemo povezati sa svim vrhovima osim sa njime samim, a sa svoja dva susjedna vrha daje stranice, a ne dijagonale). I jos nismo brojali duzinu  , koja je u
, koja je u  -terokutu stranica, ali u
-terokutu stranica, ali u 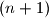 -terokutu je dijagonala.
-terokutu je dijagonala.Dakle, ukupno imamo
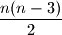 dijagonala iz
dijagonala iz  -terokuta,
-terokuta, 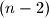 dijagonale iz tocke
dijagonale iz tocke  i dijagonalu
i dijagonalu  , sto je u sumi
, sto je u sumi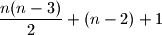
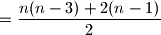
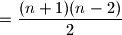
 Školjka
Školjka 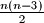 .
.