Točno
22. listopada 2013. 19:00 (12 godine, 4 mjeseci)
Sakrij rješenje
Sakrij rješenje
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
Kliknite ovdje kako biste prikazali rješenje.
Baza

Uz malo izprobavanja mozemo vidjeti da
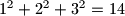
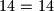
Pretpostavka
Postoje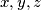 takvi da
takvi da 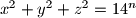
Za neki prirodni
Korak
Mozemo primjetiti da je prilicni jednostavno napraviti korak sa na
na 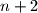 tako sto cijelu jednadzbu pomnozimo s
tako sto cijelu jednadzbu pomnozimo s 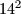
Time dobivamo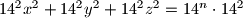
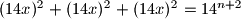
Uz ovakav korak i bazu za dokazali smo da tvrdnja vrijedi za sve neparne
dokazali smo da tvrdnja vrijedi za sve neparne  (iz cinjenice da vrijedi za
(iz cinjenice da vrijedi za  slijedi da vrijedi i za
slijedi da vrijedi i za  , pa iz toga i za
, pa iz toga i za  i tako dalje)
i tako dalje)
Kada bi pokazali da vrijedi i za , dakle konstruirali jos jednu bazu, iz te bi baze slijedilo da vrijedi za sve parne
, dakle konstruirali jos jednu bazu, iz te bi baze slijedilo da vrijedi za sve parne  , i tako bi smo pokazali da tvrdnja vrijedi za sve prirodne brojeve.
, i tako bi smo pokazali da tvrdnja vrijedi za sve prirodne brojeve.
Uz malo isprobavanja dobivamo:
Druga baza
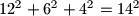
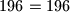

Uz malo izprobavanja mozemo vidjeti da
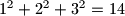
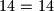
Pretpostavka
Postoje
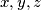 takvi da
takvi da 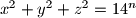
Za neki prirodni

Korak
Mozemo primjetiti da je prilicni jednostavno napraviti korak sa
 na
na 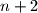 tako sto cijelu jednadzbu pomnozimo s
tako sto cijelu jednadzbu pomnozimo s 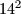
Time dobivamo
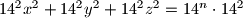
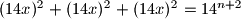
Uz ovakav korak i bazu za
 dokazali smo da tvrdnja vrijedi za sve neparne
dokazali smo da tvrdnja vrijedi za sve neparne  (iz cinjenice da vrijedi za
(iz cinjenice da vrijedi za  slijedi da vrijedi i za
slijedi da vrijedi i za  , pa iz toga i za
, pa iz toga i za  i tako dalje)
i tako dalje)Kada bi pokazali da vrijedi i za
 , dakle konstruirali jos jednu bazu, iz te bi baze slijedilo da vrijedi za sve parne
, dakle konstruirali jos jednu bazu, iz te bi baze slijedilo da vrijedi za sve parne  , i tako bi smo pokazali da tvrdnja vrijedi za sve prirodne brojeve.
, i tako bi smo pokazali da tvrdnja vrijedi za sve prirodne brojeve.Uz malo isprobavanja dobivamo:
Druga baza
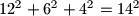
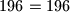
 Školjka
Školjka 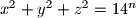 .
.