Točno
23. listopada 2013. 19:53 (12 godine, 4 mjeseci)
Sakrij rješenje
Sakrij rješenje
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
Kliknite ovdje kako biste prikazali rješenje.
Pokazati cemo da je ovo moguce, i ne samo to, nego da je moguce tako poplocati tako da nepoplocani kvadratic bude u nekom od kuteva.
Baza
Za x
x tablicu, ovo je ocito (kako god ju poplocali ostati ce tocno jedan nepoplocan, i to u kutu)
tablicu, ovo je ocito (kako god ju poplocali ostati ce tocno jedan nepoplocan, i to u kutu)
Pretpostavka
Pretpotsavima da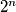 x
x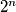 tablu mozemo poplocati kao na slici (jedini naznaceni kvadratic je onaj koij nije poplocan)
tablu mozemo poplocati kao na slici (jedini naznaceni kvadratic je onaj koij nije poplocan)

Korak
Uzmimo cetiri takva kvadrata i, uz malo rotacije, slozimo ih kao na slici
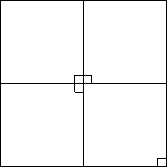
Sada je jasno da koristeci jos jednu dominu mozemo poplocati tri od preostala cetiri nepoplocana kvadrata, a ostaviti nepoplocani u kutu.
Baza
Za
 x
x tablicu, ovo je ocito (kako god ju poplocali ostati ce tocno jedan nepoplocan, i to u kutu)
tablicu, ovo je ocito (kako god ju poplocali ostati ce tocno jedan nepoplocan, i to u kutu)Pretpostavka
Pretpotsavima da
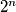 x
x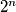 tablu mozemo poplocati kao na slici (jedini naznaceni kvadratic je onaj koij nije poplocan)
tablu mozemo poplocati kao na slici (jedini naznaceni kvadratic je onaj koij nije poplocan)
Korak
Uzmimo cetiri takva kvadrata i, uz malo rotacije, slozimo ih kao na slici

Sada je jasno da koristeci jos jednu dominu mozemo poplocati tri od preostala cetiri nepoplocana kvadrata, a ostaviti nepoplocani u kutu.
 Školjka
Školjka 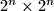 ploču, tako da se ostavi točno jedno prazno mjesto, koristeći samo domine oblika slova L sa jednakim krakovima:
ploču, tako da se ostavi točno jedno prazno mjesto, koristeći samo domine oblika slova L sa jednakim krakovima:  .
.