Točno
23. listopada 2013. 21:28 (12 godine, 4 mjeseci)
Sakrij rješenje
Sakrij rješenje
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
Kliknite ovdje kako biste prikazali rješenje.
Promatrajmo dodavanje  -og pravca. On ce, kao sto smo zakljucili u proslom zadatku imati
-og pravca. On ce, kao sto smo zakljucili u proslom zadatku imati  sjecista. Dio ravnine prije prvog sjecista dijela na dva dijela (dakle, povecao je broj za
sjecista. Dio ravnine prije prvog sjecista dijela na dva dijela (dakle, povecao je broj za  ), dio izmedu prvog i drugog isto, i tako sve do dijela nakon
), dio izmedu prvog i drugog isto, i tako sve do dijela nakon  -tog sijecista. Dakle, ukupno
-tog sijecista. Dakle, ukupno  novih djelova ravnine.
novih djelova ravnine.
Dakle, ako -ti pravc dodaje jos
-ti pravc dodaje jos  dio ravnine,
dio ravnine,  pravaca ce dijeliti na ukupno
pravaca ce dijeliti na ukupno 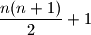
Baza

Jedan pravac ravninu dijelu u dijela,
dijela, 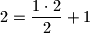 ,
, 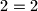
Pretpostavka
Pretpostavimo da pravaca dijeli ravninu u
pravaca dijeli ravninu u 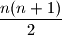 dijelova
dijelova
Korak
Dodavanjem -og pravca dobivamo jos
-og pravca dobivamo jos 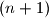 dio ravnine. Dakle, novi broj djelova ravnine je
dio ravnine. Dakle, novi broj djelova ravnine je
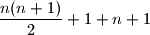
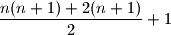
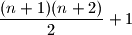
 -og pravca. On ce, kao sto smo zakljucili u proslom zadatku imati
-og pravca. On ce, kao sto smo zakljucili u proslom zadatku imati  sjecista. Dio ravnine prije prvog sjecista dijela na dva dijela (dakle, povecao je broj za
sjecista. Dio ravnine prije prvog sjecista dijela na dva dijela (dakle, povecao je broj za  ), dio izmedu prvog i drugog isto, i tako sve do dijela nakon
), dio izmedu prvog i drugog isto, i tako sve do dijela nakon  -tog sijecista. Dakle, ukupno
-tog sijecista. Dakle, ukupno  novih djelova ravnine.
novih djelova ravnine.Dakle, ako
 -ti pravc dodaje jos
-ti pravc dodaje jos  dio ravnine,
dio ravnine,  pravaca ce dijeliti na ukupno
pravaca ce dijeliti na ukupno 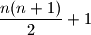
Baza

Jedan pravac ravninu dijelu u
 dijela,
dijela, 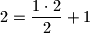 ,
, 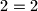
Pretpostavka
Pretpostavimo da
 pravaca dijeli ravninu u
pravaca dijeli ravninu u 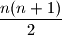 dijelova
dijelovaKorak
Dodavanjem
 -og pravca dobivamo jos
-og pravca dobivamo jos 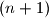 dio ravnine. Dakle, novi broj djelova ravnine je
dio ravnine. Dakle, novi broj djelova ravnine je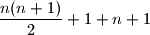
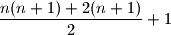
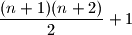
 Školjka
Školjka