Točno
29. listopada 2013. 16:24 (12 godine, 4 mjeseci)
Sakrij rješenje
Sakrij rješenje
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
Kliknite ovdje kako biste prikazali rješenje.
U svakom koraku umjesto broja pisemo sumu njegovih znamenaka. Suma znamenaka nas naravno podsjeca na mod  i mod
i mod  . Ocito je da je svaki korak inavrijantan s obzirom na ostatak pri djeljenju s oba ta broja. Ostatak pri djeljenju s
. Ocito je da je svaki korak inavrijantan s obzirom na ostatak pri djeljenju s oba ta broja. Ostatak pri djeljenju s  nam odmah govori i koji ce konkretan jednoznamenkas broj svaki pocetni broj postati.
nam odmah govori i koji ce konkretan jednoznamenkas broj svaki pocetni broj postati.
Kako broj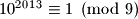 , jedinica je ocito vise. Potrebno je jos samo provejriti koliko ima brojeva koji daju koji ostatak pri djeljenju s
, jedinica je ocito vise. Potrebno je jos samo provejriti koliko ima brojeva koji daju koji ostatak pri djeljenju s  . Jedinica ima
. Jedinica ima 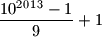 , a dvojki
, a dvojki 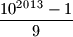 .
.
 i mod
i mod  . Ocito je da je svaki korak inavrijantan s obzirom na ostatak pri djeljenju s oba ta broja. Ostatak pri djeljenju s
. Ocito je da je svaki korak inavrijantan s obzirom na ostatak pri djeljenju s oba ta broja. Ostatak pri djeljenju s  nam odmah govori i koji ce konkretan jednoznamenkas broj svaki pocetni broj postati.
nam odmah govori i koji ce konkretan jednoznamenkas broj svaki pocetni broj postati. Kako broj
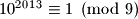 , jedinica je ocito vise. Potrebno je jos samo provejriti koliko ima brojeva koji daju koji ostatak pri djeljenju s
, jedinica je ocito vise. Potrebno je jos samo provejriti koliko ima brojeva koji daju koji ostatak pri djeljenju s  . Jedinica ima
. Jedinica ima 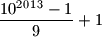 , a dvojki
, a dvojki 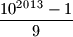 .
.  Školjka
Školjka  do
do 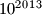 . U svakom koraku obrišemo sve brojeve i umjesto svakog od njih napišemo sumu znamenaka obrisanog broja. Postupak ponavljamo dok svi brojevi na ploći nisu jednoznamenkasti. Ima li više brojeva
. U svakom koraku obrišemo sve brojeve i umjesto svakog od njih napišemo sumu znamenaka obrisanog broja. Postupak ponavljamo dok svi brojevi na ploći nisu jednoznamenkasti. Ima li više brojeva  ? Koliko ima kojih brojeva?
? Koliko ima kojih brojeva?