Točno
29. listopada 2013. 16:25 (12 godine, 4 mjeseci)
Sakrij rješenje
Sakrij rješenje
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
Kliknite ovdje kako biste prikazali rješenje.
Promatrajmo ostatak tog broja pri djeljenju s  . Prije promjene ostatak je
. Prije promjene ostatak je 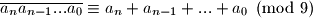 gdje su
gdje su  znamenke. Nakon promjene imamo
znamenke. Nakon promjene imamo 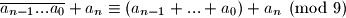 , Jasno je da je ostatak pri djeljenju s
, Jasno je da je ostatak pri djeljenju s  ostao nepromjenjen.
ostao nepromjenjen.
Kada bi deseteroznamenkasti broj imao sve znamenke razlicite, suma njegovih znamenaka bi bila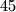 , pa bi on bio djeljiv s
, pa bi on bio djeljiv s  . Pocetni broj nije djeljiv s
. Pocetni broj nije djeljiv s  . Kontradikcija, broj ocito nema sve znamenke razlicite.
. Kontradikcija, broj ocito nema sve znamenke razlicite.
 . Prije promjene ostatak je
. Prije promjene ostatak je 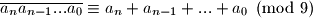 gdje su
gdje su  znamenke. Nakon promjene imamo
znamenke. Nakon promjene imamo 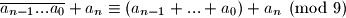 , Jasno je da je ostatak pri djeljenju s
, Jasno je da je ostatak pri djeljenju s  ostao nepromjenjen.
ostao nepromjenjen.Kada bi deseteroznamenkasti broj imao sve znamenke razlicite, suma njegovih znamenaka bi bila
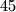 , pa bi on bio djeljiv s
, pa bi on bio djeljiv s  . Pocetni broj nije djeljiv s
. Pocetni broj nije djeljiv s  . Kontradikcija, broj ocito nema sve znamenke razlicite.
. Kontradikcija, broj ocito nema sve znamenke razlicite.  Školjka
Školjka 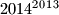 . U svakom koraku mu obrišemo najlijeviju znamenku i pridodamo je dobivenom broju (primjerice
. U svakom koraku mu obrišemo najlijeviju znamenku i pridodamo je dobivenom broju (primjerice 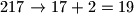 ). Ponavljamo postupak dok ne dobijemo broj od
). Ponavljamo postupak dok ne dobijemo broj od  znamenaka. Dokaži da dobiveni broj ima neke dvije znamenke jednake.
znamenaka. Dokaži da dobiveni broj ima neke dvije znamenke jednake.