Točno
29. listopada 2013. 16:26 (12 godine, 4 mjeseci)
Sakrij rješenje
Sakrij rješenje
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
Kliknite ovdje kako biste prikazali rješenje.
Kako nas zanima parnost konacnog broja, provjerimo sto se dogada sa parnosti sume u svakom koraku. Kako je 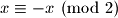 mozemo zanemariti apsolutni vrjednost.
mozemo zanemariti apsolutni vrjednost.
Kako znamo da vrijedi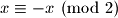 , ne samo da mozemo zanemariti apsolutnu vrijednost, nego je prilicno jasno da vrijedi i
, ne samo da mozemo zanemariti apsolutnu vrijednost, nego je prilicno jasno da vrijedi i 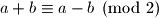 . Dakle, parnost sume se nikada ne mijenja. Pocetna suma je neparna (ovo se lagano pokaze na vise razlicitih nacina, pokusaj sam/sama :)), pa ce i konacni broj biti neparan.
. Dakle, parnost sume se nikada ne mijenja. Pocetna suma je neparna (ovo se lagano pokaze na vise razlicitih nacina, pokusaj sam/sama :)), pa ce i konacni broj biti neparan.
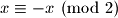 mozemo zanemariti apsolutni vrjednost.
mozemo zanemariti apsolutni vrjednost.Kako znamo da vrijedi
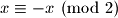 , ne samo da mozemo zanemariti apsolutnu vrijednost, nego je prilicno jasno da vrijedi i
, ne samo da mozemo zanemariti apsolutnu vrijednost, nego je prilicno jasno da vrijedi i 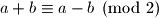 . Dakle, parnost sume se nikada ne mijenja. Pocetna suma je neparna (ovo se lagano pokaze na vise razlicitih nacina, pokusaj sam/sama :)), pa ce i konacni broj biti neparan.
. Dakle, parnost sume se nikada ne mijenja. Pocetna suma je neparna (ovo se lagano pokaze na vise razlicitih nacina, pokusaj sam/sama :)), pa ce i konacni broj biti neparan.  Školjka
Školjka  do
do 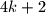 , gdje je
, gdje je  prirodan broj. Možemo odabrati neka
prirodan broj. Možemo odabrati neka  broja i obrisati oba i umjesto njih napisati
broja i obrisati oba i umjesto njih napisati 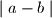 . Dokaži da, kako god birali, na kraju će ostati neparan broj.
. Dokaži da, kako god birali, na kraju će ostati neparan broj.