Školjka Točno
29. listopada 2013. 16:27 (10 godine, 6 mjeseci)
Sakrij rješenje
Sakrij rješenje
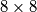šahovnica obojana je crno bijelo na način da je samo gornji lijevi kut crn, a sva ostala polja su bijela. U svakom koraku možemo promijeniti boju svih polja u jednom stupcu ili u jednom retku ili promjeniti boju svih polja u nekom 
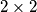kvadratu. Možemo li doći do pozicije u kojoj više nema crnih polja? A do pozicije u kojoj su sva polja crna? Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
Kliknite ovdje kako biste prikazali rješenje.
Prvo primjetimo da ako mozemo doci do pozicije da je cijela tabla crna, mozemo doci i do pozicije da crnih polja nema. Dakle, dovoljno je dokazati da je moguce ili nemoguce doci do jedne od te dvije pozicije.
Svaka od mogucih promjena djeluje na paran broj polja, pa je ocito da se ponovno parnost broja crnih polja ne mijenja. Kako je na pocetku broj crnih polja neparan, a na kraju zelimo da bude paran, to ocito nije moguce.
Svaka od mogucih promjena djeluje na paran broj polja, pa je ocito da se ponovno parnost broja crnih polja ne mijenja. Kako je na pocetku broj crnih polja neparan, a na kraju zelimo da bude paran, to ocito nije moguce.