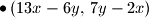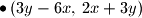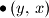Točno
29. listopada 2013. 16:28 (12 godine, 4 mjeseci)
Sakrij rješenje
Sakrij rješenje
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
Kliknite ovdje kako biste prikazali rješenje.
U zadacima ovog tipa, uvjek je korisno pokusati pronaci  takav da je suma modulo
takav da je suma modulo  invarijantna. To se radi na sljedeci nacin:
invarijantna. To se radi na sljedeci nacin:
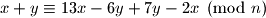
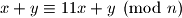
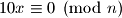
Kako ovo mora vrjediti za svaki , znamo da
, znamo da  mora biti djeljitelj od broja
mora biti djeljitelj od broja  .
.
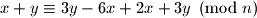
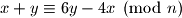
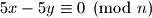
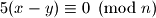
Kako ovo mora vrjediti za sve i
i  , znamo da
, znamo da  mora biti djeljitelj broja
mora biti djeljitelj broja  .
.
Dakle, da bi prva promjena bila invarijantna modulo ,
, 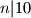 , da bi druga promjena bila invarijantna modulo
, da bi druga promjena bila invarijantna modulo  ,
, 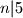 . Ocito jedini brojevi koji ovo zadovoljavaju su
. Ocito jedini brojevi koji ovo zadovoljavaju su  i
i  . Kako je gledati ostatke pri djeljenju s
. Kako je gledati ostatke pri djeljenju s  malo besmisleno, gledamo ostatke pri djleljenju s
malo besmisleno, gledamo ostatke pri djleljenju s  .
.
Znamo da se suma mod ne mijenja. Na pocetku je suma jednaka
ne mijenja. Na pocetku je suma jednaka  , a na kraju
, a na kraju  . Ta dva broja ne daju isti ostatak pri djeljenju s
. Ta dva broja ne daju isti ostatak pri djeljenju s  , pa je nemoguce doci iz uredenog para
, pa je nemoguce doci iz uredenog para 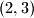 u
u 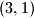 .
.
 takav da je suma modulo
takav da je suma modulo  invarijantna. To se radi na sljedeci nacin:
invarijantna. To se radi na sljedeci nacin: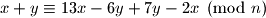
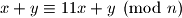
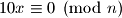
Kako ovo mora vrjediti za svaki
 , znamo da
, znamo da  mora biti djeljitelj od broja
mora biti djeljitelj od broja  .
.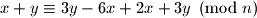
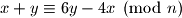
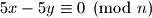
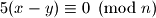
Kako ovo mora vrjediti za sve
 i
i  , znamo da
, znamo da  mora biti djeljitelj broja
mora biti djeljitelj broja  .
. Dakle, da bi prva promjena bila invarijantna modulo
 ,
, 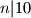 , da bi druga promjena bila invarijantna modulo
, da bi druga promjena bila invarijantna modulo  ,
, 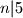 . Ocito jedini brojevi koji ovo zadovoljavaju su
. Ocito jedini brojevi koji ovo zadovoljavaju su  i
i  . Kako je gledati ostatke pri djeljenju s
. Kako je gledati ostatke pri djeljenju s  malo besmisleno, gledamo ostatke pri djleljenju s
malo besmisleno, gledamo ostatke pri djleljenju s  .
.Znamo da se suma mod
 ne mijenja. Na pocetku je suma jednaka
ne mijenja. Na pocetku je suma jednaka  , a na kraju
, a na kraju  . Ta dva broja ne daju isti ostatak pri djeljenju s
. Ta dva broja ne daju isti ostatak pri djeljenju s  , pa je nemoguce doci iz uredenog para
, pa je nemoguce doci iz uredenog para 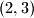 u
u 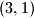 .
.  Školjka
Školjka  možemo preći u bilo koju od sljedećih točaka:
možemo preći u bilo koju od sljedećih točaka: