Točno
29. listopada 2013. 16:29 (12 godine, 4 mjeseci)
Sakrij rješenje
Sakrij rješenje
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
Kliknite ovdje kako biste prikazali rješenje.
Pokusajmo ponovo pronaci  takav da je suma modulo
takav da je suma modulo  invarijantna.
invarijantna.
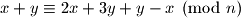
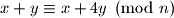
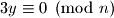
Kako ovo mora vrjediti za sve , znamo da
, znamo da 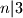 . Pa promotrimo dali je i druga promjena invarijantna modulo
. Pa promotrimo dali je i druga promjena invarijantna modulo  .
.
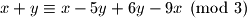
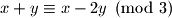
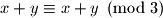
Kako svi moguci koraci ostavljaju sumu invarijantnu mod , potrebno je jos samo provjeriti pocetni i zavrsni par koji smo dobili. Na pocetku je suma djeljiva s
, potrebno je jos samo provjeriti pocetni i zavrsni par koji smo dobili. Na pocetku je suma djeljiva s  , a na kraju daje ostatak
, a na kraju daje ostatak  pri djeljenju s
pri djeljenju s  . Dakle, nemoguce je.
. Dakle, nemoguce je.
 takav da je suma modulo
takav da je suma modulo  invarijantna.
invarijantna.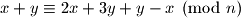
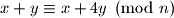
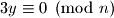
Kako ovo mora vrjediti za sve
 , znamo da
, znamo da 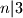 . Pa promotrimo dali je i druga promjena invarijantna modulo
. Pa promotrimo dali je i druga promjena invarijantna modulo  .
.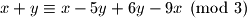
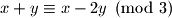
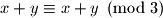
Kako svi moguci koraci ostavljaju sumu invarijantnu mod
 , potrebno je jos samo provjeriti pocetni i zavrsni par koji smo dobili. Na pocetku je suma djeljiva s
, potrebno je jos samo provjeriti pocetni i zavrsni par koji smo dobili. Na pocetku je suma djeljiva s  , a na kraju daje ostatak
, a na kraju daje ostatak  pri djeljenju s
pri djeljenju s  . Dakle, nemoguce je.
. Dakle, nemoguce je.  Školjka
Školjka  možemo primjeniti sljedeće promjene:
možemo primjeniti sljedeće promjene: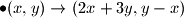
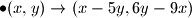
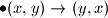
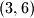 , možemo li dobiti
, možemo li dobiti 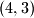 ?
?