Točno
29. listopada 2013. 16:29 (12 godine, 4 mjeseci)
Sakrij rješenje
Imamo

bijelih,

crvenih i

plavih žetona. U svakom koraku možemo uzeti po jedan sa neke dvije hrpe, i staviti jedan na treću hrpu. Dokaži da za fiksne
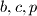
, kojim god redom radili ovo, ako dođemo do samo jednog žetona on će uvijek biti iste boje.
%V0
Imamo $b$ bijelih, $c$ crvenih i $p$ plavih žetona. U svakom koraku možemo uzeti po jedan sa neke dvije hrpe, i staviti jedan na treću hrpu. Dokaži da za fiksne $b,c,p$, kojim god redom radili ovo, ako dođemo do samo jednog žetona on će uvijek biti iste boje.
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
Primjetimo da se u svakom koraku mijenja parnost svake hrpe. Dakle, da bi na kraju ostao tocno jedan, jedna hrpa mora biti razlicite parnosti od druge dvije, i ocito je da ce onda tocno na toj razlicitoj hrpi ostati tocno

, ako ostane na ijednoj.
%V0
Primjetimo da se u svakom koraku mijenja parnost svake hrpe. Dakle, da bi na kraju ostao tocno jedan, jedna hrpa mora biti razlicite parnosti od druge dvije, i ocito je da ce onda tocno na toj razlicitoj hrpi ostati tocno $1$, ako ostane na ijednoj.
| 31. listopada 2013. 22:44 | ikicic | Točno |