Točno
12. travnja 2012. 23:05 (13 godine, 10 mjeseci)
Ako su

i

kompleksni brojevi, dokaži nejednakost
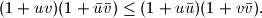
%V0
Ako su $u$ i $v$ kompleksni brojevi, dokaži nejednakost $$
(1+uv)(1+\bar{u}\bar{v})\leq (1+u\bar{u})(1+v\bar{v}).
$$
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
%V0
$$(1 + uv)(1 + \bar u \bar v) \leq (1 + u\bar u)(1 + v\bar v)$$ $$\Updownarrow$$ $$1 + uv + \bar u \bar v + |u|^2|v|^2 \leq 1 + u\bar u + v\bar v + |u|^2|v|^2$$ $$\Updownarrow$$ $$uv + \bar u \bar v \leq u \bar u + v \bar v$$ $$\Updownarrow$$ $$0 \leq (u - \bar v)(\bar u - v)$$ $$\Updownarrow$$ $$0 \leq |u - \bar v|^2$$
| 13. travnja 2012. 00:51 | grga | Točno |