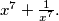Neocijenjeno
8. kolovoza 2024. 17:04 (1 godina, 5 mjeseci)
Ako je 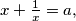 izračunajte
izračunajte 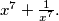
Ako je $x + \frac{1}{x} = a,$ izračunajte $x^7 + \frac{1}{x^7}.$
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
Očigledno bi bilo suludo potencirati danu jednadžbu "na sedmu" pa moramo pronaći obilaznicu. Na primjer, možemo kvadrirati i kubirati danu jednadžbu jer će se, ako gledamo gdje će nas to odvesti, neki članovi pokratiti. Dakle, to mora biti neki trag. Dobijemo:
$$\left(x+\frac{1}{x}\right)^2 = x^2 + \underbrace{2 \cdot x \cdot \frac{1}{x}}_\text{krati se!} + \left(\frac{1}{x}\right)^2 = x^2 + \frac{1}{x^2}+ 2 = a^2 \Rightarrow x^2 + \frac{1}{x^2} = a^2 - 2$$
$$\left(x+\frac{1}{x}\right)^3 = x^3 + 3 \cdot x^2 \cdot \frac{1}{x} + 3 \cdot x \cdot \left(\frac{1}{x}\right)^2 + \left(\frac{1}{x}\right)^3 = x^3 + \frac{1}{x^3}+3x+\frac{3}{x}=a^3$$
$$x^3 + \frac{1}{x^3}+3\underbrace{\left(x+\frac{1}{x}\right)}_\text{početna jednadžba}=a^3 \Rightarrow x^3 + \frac{1}{x^3} = a^{3}-3a$$
Sada, moramo smisliti način na koji ćemo manipulirati s dobivenim jednadžbama. Metodom pokušaja i pogreške, primijetimo da nas množenje jednadžbi dovodi do:
$$\left(x^{2}+\frac{1}{x^2}\right)\left(x^{3}+\frac{1}{x^3}\right) = x^{5} + \frac{1}{x^2} \cdot x^3 +x^2 \cdot \frac{1}{x^3}+\frac{1}{x^5}=x^{5} + x + \frac{1}{x}+\frac{1}{x^5}$$
$$x^{5} +\frac{1}{x^5}+\underbrace{\left(x+\frac{1}{x}\right)}_\text{početna jednadžba} = \left(a^3-3a\right)\left(a^2-2\right) \Rightarrow x^{5} +\frac{1}{x^5} =\left(a^3-3a\right)\left(a^2-2\right)-a$$
Sada je potrebno doći do reda veličine $7$, a to možemo tako da (ne preostaje ništa drugo, a nakon prethodnog koraka, nameće se intuitivno) pomnožimo nešto sadrži $x^5$ i $x^2$ pa slijedi:
$$\left(x^{2}+\frac{1}{x^2}\right)\left(x^{5}+\frac{1}{x^5}\right)= x^{7} + \frac{1}{x^2} \cdot x^5 +x^2 \cdot \frac{1}{x^5}+\frac{1}{x^7}=x^{7} + x^{3} + \frac{1}{x^3}+\frac{1}{x^7}$$
$$x^{7} +\frac{1}{x^7}+\underbrace{x^{3} + \frac{1}{x^3}}_\text{znamo!} = (a^2-2)\left(\left(a^3-3a\right)\left(a^2-2\right)-a\right)$$
$$\Rightarrow x^{7} +\frac{1}{x^7} = (a^2-2)\left(\left(a^3-3a\right)\left(a^2-2\right)-a\right) - a^3 +3a$$
Sređivanjem se dobije:
$$ x^{7} +\frac{1}{x^7} = (a^2-2)\left(a^5-3a^3-2a^3+6a-a\right) - a^3 +3a$$
$$ \Leftrightarrow (a^2-2)\left(a^5-5a^3+5a\right) - a^3 +3a$$
$$ \Leftrightarrow a(a^2-2)\left(a^4-5a^2+5\right) - a\left(a^2 -3\right)$$
$$ \Leftrightarrow a\left((a^2-2)\left(a^4-5a^2+5\right) - \left(a^2 -3\right)\right)$$
$$ \Leftrightarrow a\left((a^2-2)\left(a^4-5a^2+5\right) - \left(a^2 -3\right)\right)$$
$$ \Leftrightarrow a\left(a^6-2a^4-5a^4+10a^2+5a^2-10 - a^2 +3\right)$$
$$ \Leftrightarrow a\left(a^6-7a^4+14a^2-7\right)$$
$$ x^{7} +\frac{1}{x^7} = a\left(a^6-7a^4+14a^2-7\right) = a^7-7a^5+14a^3-7a$$
što je i trebalo izračunati. Zapamtimo da manipulacije u matematici čine čuda!
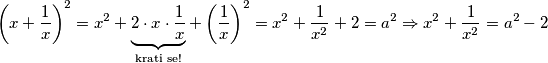
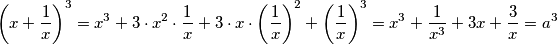
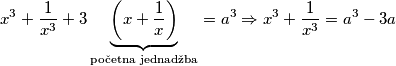 Sada, moramo smisliti način na koji ćemo manipulirati s dobivenim jednadžbama. Metodom pokušaja i pogreške, primijetimo da nas množenje jednadžbi dovodi do:
Sada, moramo smisliti način na koji ćemo manipulirati s dobivenim jednadžbama. Metodom pokušaja i pogreške, primijetimo da nas množenje jednadžbi dovodi do: 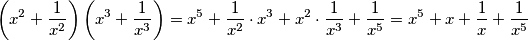
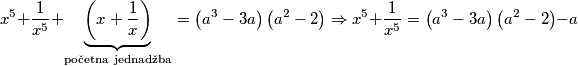 Sada je potrebno doći do reda veličine
Sada je potrebno doći do reda veličine  , a to možemo tako da (ne preostaje ništa drugo, a nakon prethodnog koraka, nameće se intuitivno) pomnožimo nešto sadrži
, a to možemo tako da (ne preostaje ništa drugo, a nakon prethodnog koraka, nameće se intuitivno) pomnožimo nešto sadrži 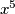 i
i  pa slijedi:
pa slijedi: 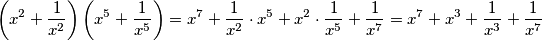
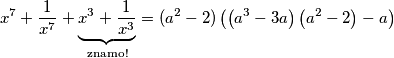
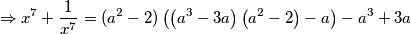 Sređivanjem se dobije:
Sređivanjem se dobije: 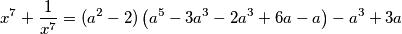
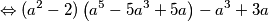
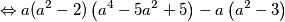
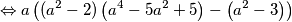
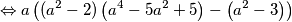
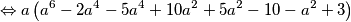
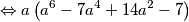
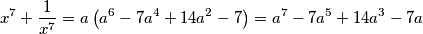 što je i trebalo izračunati. Zapamtimo da manipulacije u matematici čine čuda!
što je i trebalo izračunati. Zapamtimo da manipulacije u matematici čine čuda!  Školjka
Školjka 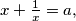 izračunajte
izračunajte