Neocijenjeno
8. kolovoza 2024. 17:05 (1 godina, 6 mjeseci)
U Gaussovoj kompleksnoj ravnini skicirajte skup točaka kojima pripadaju kompleksni brojevi koji zadovoljavaju uvjet: 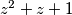 je pozitivan realan broj.
je pozitivan realan broj.
U Gaussovoj kompleksnoj ravnini skicirajte skup točaka kojima pripadaju kompleksni brojevi koji zadovoljavaju uvjet: $z^2 + z + 1$ je pozitivan realan broj.
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
Ukoliko bi zaključili $z^2+z+1>0$, $\forall z \in \mathbb{C}$,napravili bi grešku jer relacija uređaja ne vrijedi na skupu kompleksnih brojeva (npr. nejednakost $i > -1$ nema značenja - o njoj ne možemo ništa reći). \\ Dakle, zapišimo broj $z = x + yi$, $x,y \in \mathbb{R}, i^{2} = -1$. Uvrštavanjem u izraz slijedi:
$$(x+yi)^2 + x + yi + 1 = x^2 + 2xyi + y^2 \cdot i^2 + x + yi + 1 = x^2 +x+ y^2-1 + i\left(2xy+y\right)$$
Kako bi taj broj bio realan, mora vrijediti da je:
$$\mbox{Im} \left(z^2+z+1\right) = 0 \Rightarrow 2xy+y=0$$
i to pozitivan:
$$\mbox{Re} \left(z^2+z+1\right) > 0 \Rightarrow x^2 + x - y^2 +1 > 0.$$
Dobiva se sustav:
$\begin{cases}
2xy+y=0, \\
x^2 + x - y^2 +1 > 0 \\
\end{cases}$.
\\
Jednadžba se može napisati u obliku: $$y(2x+1)=0 \Rightarrow \begin{matrix}y=0\\ 2x+1=0\Rightarrow x = -\frac{1}{2} \end{matrix}.$$
Dakle, imamo dva slučaja:\\
1. ako je $y = 0$
$$x^2+x+1>0,$$
što očigledno vrijedi za bilo koji realni broj $x$.\\
2. ako je $x =-\frac{1}{2}$
$$\left(-\frac{1}{2}\right)^2-\frac{1}{2}-y^2+1>0 \Rightarrow -y^2 > - \frac{3}{4} \Rightarrow \left|y\right|< \frac{\sqrt{3}}{2}.$$
Dakle, u Gaussovoj ravnini bit će prikazana unija dva pravca:
$$\begin{matrix} y = 0, \forall x \in \mathbb{R} \\ -\frac{\sqrt{3}}{2}<y <\frac{\sqrt{3}}{2} , x =-\frac{1}{2} \end{matrix}.$$
Za vježbu ih nacrtajte!
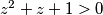 ,
, 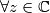 ,napravili bi grešku jer relacija uređaja ne vrijedi na skupu kompleksnih brojeva (npr. nejednakost
,napravili bi grešku jer relacija uređaja ne vrijedi na skupu kompleksnih brojeva (npr. nejednakost 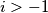 nema značenja - o njoj ne možemo ništa reći).
nema značenja - o njoj ne možemo ništa reći). 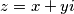 ,
, 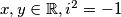 . Uvrštavanjem u izraz slijedi:
. Uvrštavanjem u izraz slijedi: 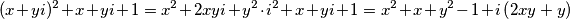 Kako bi taj broj bio realan, mora vrijediti da je:
Kako bi taj broj bio realan, mora vrijediti da je: 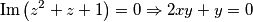 i to pozitivan:
i to pozitivan: 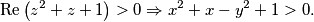 Dobiva se sustav:
Dobiva se sustav: 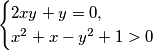 .
. 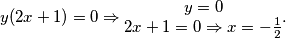 Dakle, imamo dva slučaja:
Dakle, imamo dva slučaja: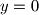
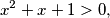 što očigledno vrijedi za bilo koji realni broj
što očigledno vrijedi za bilo koji realni broj  .
.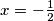
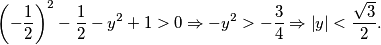 Dakle, u Gaussovoj ravnini bit će prikazana unija dva pravca:
Dakle, u Gaussovoj ravnini bit će prikazana unija dva pravca: 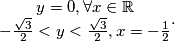 Za vježbu ih nacrtajte!
Za vježbu ih nacrtajte!  Školjka
Školjka 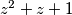 je pozitivan realan broj.
je pozitivan realan broj.