Neocijenjeno
16. kolovoza 2024. 19:03 (1 godina, 6 mjeseci)
Ako koeficijenti jednadžbi $x^2 + px + q = 0$ i $x^2 + mx + n = 0$ zadovoljavaju uvjet $mp = 2(n + q)$ dokažite da su rješenja bar jedne od njih realna.
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
Diskriminante kvadratni jednadžbi redom iznose: 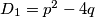 i
i 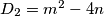 . Naime, zbrajanjem obje diskriminante dobijemo (nazovimo ga) izraz
. Naime, zbrajanjem obje diskriminante dobijemo (nazovimo ga) izraz  , tj.:
, tj.: 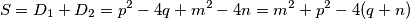 Iz zadane jednakosti
Iz zadane jednakosti 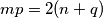 slijedi da je
slijedi da je 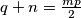 pa se izraz
pa se izraz  može zapisati u obliku:
može zapisati u obliku: 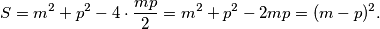 Prema tome,
Prema tome, 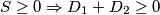 ,
, 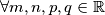 .
.
Kvadratna jednadžba ima realna rješenja (ne nužno različita) ako je njezina diskriminanta veća od nule ili jednaka nuli.
Ako pretpostavimo suprotno, da nijedna kvadratna jednadžba nema realna rješenja, tj. ako je 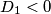 i
i 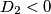 , onda je to u kontradikciji sa
, onda je to u kontradikciji sa 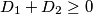 . Dakle, nije moguće da obje jednadžbe imaju kompleksna, nerealna rješenja. Drugim riječima, barem jedna od njih ima realna rješenja, kako je i trebalo dokazati.
. Dakle, nije moguće da obje jednadžbe imaju kompleksna, nerealna rješenja. Drugim riječima, barem jedna od njih ima realna rješenja, kako je i trebalo dokazati.
Diskriminante kvadratni jednadžbi redom iznose: $D_{1} = p^{2}-4q$ i $D_{2} = m^{2}-4n$. Naime, zbrajanjem obje diskriminante dobijemo (nazovimo ga) izraz $S$, tj.:
$$S= D_{1}+D_{2} = p^2 - 4q + m^{2}-4n = m^{2} + p^{2} - 4(q+n)$$
Iz zadane jednakosti $mp = 2(n+q)$ slijedi da je $q+n=\frac{mp}{2}$ pa se izraz $S$ može zapisati u obliku:
$$S= m^{2} + p^{2} - 4 \cdot \frac{mp}{2} = m^{2}+p^{2}-2mp=(m-p)^2.$$
Prema tome, $S \geq 0 \Rightarrow D_{1}+D_{2}\geq0$, $\forall m,n,p,q \in \mathbb{R}$.\\
Kvadratna jednadžba ima realna rješenja (ne nužno različita) ako je njezina diskriminanta veća od nule ili jednaka nuli.\\
Ako pretpostavimo suprotno, da nijedna kvadratna jednadžba nema realna rješenja, tj. ako je $D_{1} < 0$ i $D_{2} < 0$, onda je to u kontradikciji sa $D_{1}+D_{2} \geq 0$. Dakle, nije moguće da obje jednadžbe imaju kompleksna, nerealna rješenja. Drugim riječima, barem jedna od njih ima realna rješenja, kako je i trebalo dokazati.
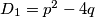 i
i 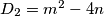 . Naime, zbrajanjem obje diskriminante dobijemo (nazovimo ga) izraz
. Naime, zbrajanjem obje diskriminante dobijemo (nazovimo ga) izraz  , tj.:
, tj.: 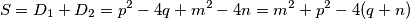 Iz zadane jednakosti
Iz zadane jednakosti 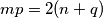 slijedi da je
slijedi da je 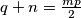 pa se izraz
pa se izraz  može zapisati u obliku:
može zapisati u obliku: 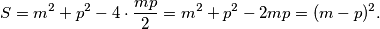 Prema tome,
Prema tome, 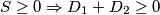 ,
, 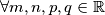 .
.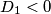 i
i 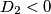 , onda je to u kontradikciji sa
, onda je to u kontradikciji sa 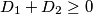 . Dakle, nije moguće da obje jednadžbe imaju kompleksna, nerealna rješenja. Drugim riječima, barem jedna od njih ima realna rješenja, kako je i trebalo dokazati.
. Dakle, nije moguće da obje jednadžbe imaju kompleksna, nerealna rješenja. Drugim riječima, barem jedna od njih ima realna rješenja, kako je i trebalo dokazati.  Školjka
Školjka 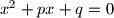 i
i 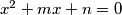 zadovoljavaju uvjet
zadovoljavaju uvjet 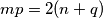 dokažite da su rješenja bar jedne od njih realna.
dokažite da su rješenja bar jedne od njih realna.