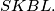Nacrtajte skicu zadatka sa svim zadanim oznakama.
Za površinu trapeza 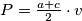 potrebna nam je duljina osnovica i visine. Dakle, potrebno je odrediti što je što! S obzirom na to da je pravac
potrebna nam je duljina osnovica i visine. Dakle, potrebno je odrediti što je što! S obzirom na to da je pravac 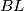 paralelan sa
paralelan sa 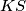 jer su oba okomita na pravac
jer su oba okomita na pravac 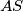 , onda su osnovica trapeza
, onda su osnovica trapeza 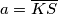 i
i 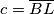 . Visina je najkraća duljina koja spaja te dvije dužine, a okomita je na obje pa mora biti dio pravca
. Visina je najkraća duljina koja spaja te dvije dužine, a okomita je na obje pa mora biti dio pravca 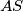 . Sada je očito da je
. Sada je očito da je  .
.
Promotrimo 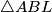 kojem je jedan kut
kojem je jedan kut 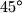 , a drugi pravi. Dakle, to je jednakokračni pravokutni trokut kojem su katete visina i kraća osnovica trapeza čiju površinu tražimo, a hipotenuza radijus kruga. Dakle,
, a drugi pravi. Dakle, to je jednakokračni pravokutni trokut kojem su katete visina i kraća osnovica trapeza čiju površinu tražimo, a hipotenuza radijus kruga. Dakle, 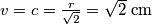 .
.
Nadalje, preostaje nam samo dobiti duljinu  . Možemo doći do nje preko sličnosti trokuta ili trigonometrije.
. Možemo doći do nje preko sličnosti trokuta ili trigonometrije.
Prvi način: SLIČNOST TROKUTA
"Ogradimo" trokute 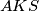 i
i 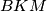 , gdje je
, gdje je  točka u kojoj se siječe okomica na pravac
točka u kojoj se siječe okomica na pravac 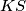 kroz točku
kroz točku  . Ovom konstrukcijom dobijemo dva prava kuta (u vrhovima
. Ovom konstrukcijom dobijemo dva prava kuta (u vrhovima  i
i  ) i zajednički kut u vrhu
) i zajednički kut u vrhu  . Prema tome, vrijedi
. Prema tome, vrijedi 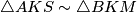 po
po  poučku. Iz koeficijenta sličnosti slijedi da vrijedi (i uz činjenicu da je četverokut
poučku. Iz koeficijenta sličnosti slijedi da vrijedi (i uz činjenicu da je četverokut 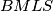 kvadrat - dovoljno je izračunati duljine stranica tog četverokuta i vidjeti da je između njih pravi kut):
kvadrat - dovoljno je izračunati duljine stranica tog četverokuta i vidjeti da je između njih pravi kut): 
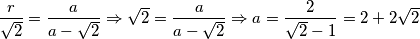 Sada je površina trapeza:
Sada je površina trapeza: 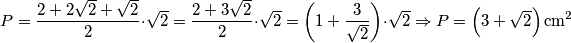 Drugi način: TRIGONOMETRIJA
Drugi način: TRIGONOMETRIJA
Neka je  . Primijetimo da je
. Primijetimo da je  jednakokračan jer su mu dvije stranice zapravo radijus kružnice, a nasuprot tih stranica jednaki su kutovi. Dakle, možemo pisati
jednakokračan jer su mu dvije stranice zapravo radijus kružnice, a nasuprot tih stranica jednaki su kutovi. Dakle, možemo pisati 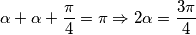 . Naime, sam taj kut iznosi
. Naime, sam taj kut iznosi 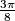 , ali vrijednosti trigonometrijskih funkcija ne znamo "napamet". Zato se možemo poslužiti sljedećim trikom, ali najprije vidimo da u pravokutnom trokutu
, ali vrijednosti trigonometrijskih funkcija ne znamo "napamet". Zato se možemo poslužiti sljedećim trikom, ali najprije vidimo da u pravokutnom trokutu  vrijedi:
vrijedi: 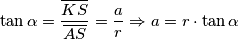 . Prema tome, potrebna nam je samo vrijednost tangensa kuta
. Prema tome, potrebna nam je samo vrijednost tangensa kuta  . Naime, vrijedi (za
. Naime, vrijedi (za 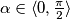 ):
): 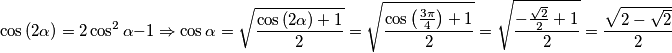 i istovremeno je (uvjet je pravokutni trokut, što nam je ostvareno):
i istovremeno je (uvjet je pravokutni trokut, što nam je ostvareno): 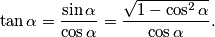 Uvrštavanjem, dobije se:
Uvrštavanjem, dobije se: 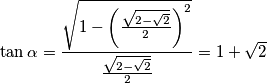 Dakle, duljina osnovice
Dakle, duljina osnovice  jednaka je:
jednaka je: 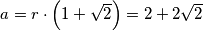 Postupak za površinu je analogan.
Postupak za površinu je analogan.
Nacrtajte skicu zadatka sa svim zadanim oznakama. \\
Za površinu trapeza $P = \frac{a+c}{2} \cdot v$ potrebna nam je duljina osnovica i visine. Dakle, potrebno je odrediti što je što! S obzirom na to da je pravac $BL$ paralelan sa $KS$ jer su oba okomita na pravac $AS$, onda su osnovica trapeza $a=\overline{KS}$ i $c=\overline{BL}$. Visina je najkraća duljina koja spaja te dvije dužine, a okomita je na obje pa mora biti dio pravca $AS$. Sada je očito da je $v = \overline{LS}$.\\
Promotrimo $\triangle ABL$ kojem je jedan kut $45^{\circ}$, a drugi pravi. Dakle, to je jednakokračni pravokutni trokut kojem su katete visina i kraća osnovica trapeza čiju površinu tražimo, a hipotenuza radijus kruga. Dakle, $v = c = \frac{r}{\sqrt{2}} = \sqrt{2} \mbox{ cm}$.\\
Nadalje, preostaje nam samo dobiti duljinu $a$. Možemo doći do nje preko sličnosti trokuta ili trigonometrije.\\
Prvi način: SLIČNOST TROKUTA\\
"Ogradimo" trokute $AKS$ i $BKM$, gdje je $M$ točka u kojoj se siječe okomica na pravac $KS$ kroz točku $B$. Ovom konstrukcijom dobijemo dva prava kuta (u vrhovima $S$ i $M$) i zajednički kut u vrhu $K$. Prema tome, vrijedi $\triangle AKS \sim \triangle BKM$ po $K-K$ poučku. Iz koeficijenta sličnosti slijedi da vrijedi (i uz činjenicu da je četverokut $BMLS$ kvadrat - dovoljno je izračunati duljine stranica tog četverokuta i vidjeti da je između njih pravi kut):
$$\frac{\overline{AS}}{\overline{BM}} = \frac{\overline{KS}}{\overline{KM}} \Rightarrow \frac{r}{\overline{LS}} = \frac{a}{\overline{KS}-\overline{MS}}$$
$$\frac{r}{\sqrt{2}} = \frac{a}{a-\sqrt{2}}\Rightarrow \sqrt{2} = \frac{a}{a-\sqrt{2}} \Rightarrow a = \frac{2}{\sqrt{2}-1} = 2+2\sqrt{2}$$
Sada je površina trapeza:
$$P=\frac{2+2\sqrt{2}+\sqrt{2}}{2} \cdot {\sqrt{2}} = \frac{2+3\sqrt{2}}{2} \cdot {\sqrt{2}}=\left(1+\frac{3}{\sqrt{2}}\right)\cdot\sqrt{2} \Rightarrow P = \left(3 + \sqrt{2}\right) \mbox{cm}^{2}$$
Drugi način: TRIGONOMETRIJA\\
Neka je $\angle SAK = \alpha$. Primijetimo da je $\triangle ABS$ jednakokračan jer su mu dvije stranice zapravo radijus kružnice, a nasuprot tih stranica jednaki su kutovi. Dakle, možemo pisati
$$\alpha + \alpha + \frac{\pi}{4} = \pi \Rightarrow 2\alpha = \frac{3\pi}{4}$$.
Naime, sam taj kut iznosi $\frac{3\pi}{8}$, ali vrijednosti trigonometrijskih funkcija ne znamo "napamet". Zato se možemo poslužiti sljedećim trikom, ali najprije vidimo da u pravokutnom trokutu $AKS$ vrijedi: $$\tan \alpha = \frac{\overline{KS}}{\overline{AS}} = \frac{a}{r} \Rightarrow a = r \cdot \tan \alpha$$.
Prema tome, potrebna nam je samo vrijednost tangensa kuta $\alpha$.
Naime, vrijedi (za $\alpha \in \langle 0, \frac{\pi}{2} \rangle$):
$$\cos\left(2\alpha\right) = 2\cos^{2}\alpha - 1 \Rightarrow \cos\alpha = \sqrt{\frac{\cos\left(2\alpha\right)+1}{2}} = \sqrt{\frac{\cos\left(\frac{3\pi}{4}\right)+1}{2}}=\sqrt{\frac{-\frac{\sqrt{2}}{2}+1}{2}} = \frac{\sqrt{2-\sqrt{2}}}{2}$$
i istovremeno je (uvjet je pravokutni trokut, što nam je ostvareno):
$$\tan\alpha=\frac{\sin\alpha}{\cos\alpha}=\frac{\sqrt{1-\cos^{2}\alpha}}{\cos\alpha}.$$
Uvrštavanjem, dobije se:
$$\tan\alpha=\frac{\sqrt{1-\left(\frac{\sqrt{2-\sqrt{2}}}{2}\right)^{2}}}{\frac{\sqrt{2-\sqrt{2}}}{2}}=1+\sqrt{2}$$
Dakle, duljina osnovice $a$ jednaka je:
$$a = r \cdot \left(1+\sqrt{2}\right) = 2 + 2\sqrt{2}$$
Postupak za površinu je analogan.
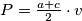 potrebna nam je duljina osnovica i visine. Dakle, potrebno je odrediti što je što! S obzirom na to da je pravac
potrebna nam je duljina osnovica i visine. Dakle, potrebno je odrediti što je što! S obzirom na to da je pravac 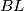 paralelan sa
paralelan sa 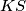 jer su oba okomita na pravac
jer su oba okomita na pravac 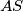 , onda su osnovica trapeza
, onda su osnovica trapeza 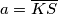 i
i 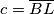 . Visina je najkraća duljina koja spaja te dvije dužine, a okomita je na obje pa mora biti dio pravca
. Visina je najkraća duljina koja spaja te dvije dužine, a okomita je na obje pa mora biti dio pravca 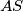 . Sada je očito da je
. Sada je očito da je  .
.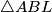 kojem je jedan kut
kojem je jedan kut 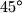 , a drugi pravi. Dakle, to je jednakokračni pravokutni trokut kojem su katete visina i kraća osnovica trapeza čiju površinu tražimo, a hipotenuza radijus kruga. Dakle,
, a drugi pravi. Dakle, to je jednakokračni pravokutni trokut kojem su katete visina i kraća osnovica trapeza čiju površinu tražimo, a hipotenuza radijus kruga. Dakle, 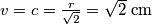 .
. . Možemo doći do nje preko sličnosti trokuta ili trigonometrije.
. Možemo doći do nje preko sličnosti trokuta ili trigonometrije. i
i  , gdje je
, gdje je  točka u kojoj se siječe okomica na pravac
točka u kojoj se siječe okomica na pravac 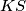 kroz točku
kroz točku  . Ovom konstrukcijom dobijemo dva prava kuta (u vrhovima
. Ovom konstrukcijom dobijemo dva prava kuta (u vrhovima  i
i  ) i zajednički kut u vrhu
) i zajednički kut u vrhu  . Prema tome, vrijedi
. Prema tome, vrijedi 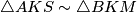 po
po  poučku. Iz koeficijenta sličnosti slijedi da vrijedi (i uz činjenicu da je četverokut
poučku. Iz koeficijenta sličnosti slijedi da vrijedi (i uz činjenicu da je četverokut 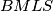 kvadrat - dovoljno je izračunati duljine stranica tog četverokuta i vidjeti da je između njih pravi kut):
kvadrat - dovoljno je izračunati duljine stranica tog četverokuta i vidjeti da je između njih pravi kut): 
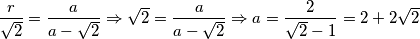 Sada je površina trapeza:
Sada je površina trapeza: 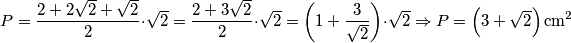 Drugi način: TRIGONOMETRIJA
Drugi način: TRIGONOMETRIJA . Primijetimo da je
. Primijetimo da je  jednakokračan jer su mu dvije stranice zapravo radijus kružnice, a nasuprot tih stranica jednaki su kutovi. Dakle, možemo pisati
jednakokračan jer su mu dvije stranice zapravo radijus kružnice, a nasuprot tih stranica jednaki su kutovi. Dakle, možemo pisati 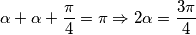 . Naime, sam taj kut iznosi
. Naime, sam taj kut iznosi 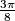 , ali vrijednosti trigonometrijskih funkcija ne znamo "napamet". Zato se možemo poslužiti sljedećim trikom, ali najprije vidimo da u pravokutnom trokutu
, ali vrijednosti trigonometrijskih funkcija ne znamo "napamet". Zato se možemo poslužiti sljedećim trikom, ali najprije vidimo da u pravokutnom trokutu 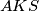 vrijedi:
vrijedi: 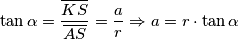 . Prema tome, potrebna nam je samo vrijednost tangensa kuta
. Prema tome, potrebna nam je samo vrijednost tangensa kuta  . Naime, vrijedi (za
. Naime, vrijedi (za 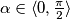 ):
): 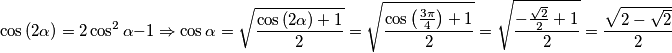 i istovremeno je (uvjet je pravokutni trokut, što nam je ostvareno):
i istovremeno je (uvjet je pravokutni trokut, što nam je ostvareno): 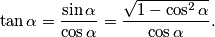 Uvrštavanjem, dobije se:
Uvrštavanjem, dobije se: 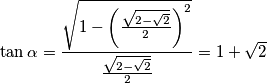 Dakle, duljina osnovice
Dakle, duljina osnovice  jednaka je:
jednaka je: 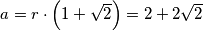 Postupak za površinu je analogan.
Postupak za površinu je analogan.  Školjka
Školjka  polumjera
polumjera 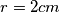 povučena su dva radijusa
povučena su dva radijusa 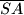 i
i 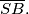 Kut među njima je
Kut među njima je 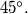 Neka je
Neka je  i okomice povučene na pravac
i okomice povučene na pravac  je nožište visine trokuta
je nožište visine trokuta 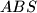 povučene iz vrha
povučene iz vrha  Izračunajte površinu trapeza
Izračunajte površinu trapeza