Točno
17. kolovoza 2024. 15:09 (1 godina, 6 mjeseci)
Ako su  i
i  realni brojevi takvi da je
realni brojevi takvi da je 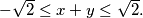
(Tekst zadatka nepotpun u originalu.)
Ako su $x$ i $y$ realni brojevi takvi da je $- \sqrt{2} \leq x + y \leq \sqrt{2}.$
\emph{(Tekst zadatka nepotpun u originalu.)}
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
Uz pronađeni dio zadatka, znamo da vrijedi $x^{2}+y^{2}=1$. Očito vrijedi $\left(x-y\right)^{2} \geq 0$, $\forall x,y \in \mathbb{R}$. Raspisivanjem, dolazimo do nejednakosti:
$$x^{2}-2xy+y^{2} \geq 0 \Rightarrow xy \leq \frac{1}{2}$$
Sada nemamo kuda (ili imamo?). Iskoristimo još jednom početnu jednadžbu (tako da stvorimo odnos između $x+y$ i $xy$):
$$x^{2}+y^{2} = x^{2}+2xy+y^{2}-2xy = (x+y)^{2}-2xy = 1 \Rightarrow xy = \frac{(x+y)^{2}-1}{2}$$
Uvrštavajući u nejednakost, dobiva se:
$$\frac{(x+y)^{2}-1}{2} \leq \frac{1}{2} \Rightarrow (x+y)^{2} \leq 2 \Rightarrow \left|x+y\right| \leq \sqrt{2} \Rightarrow -\sqrt{2} \leq x+y \leq \sqrt{2}$$
što je i trebalo dokazati.\\
Naravno, ovo je primjena AG nejednakosti.
| 17. listopada 2024. 17:47 | gabMAT | Točno |
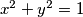 . Očito vrijedi
. Očito vrijedi 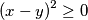 ,
, 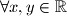 . Raspisivanjem, dolazimo do nejednakosti:
. Raspisivanjem, dolazimo do nejednakosti: 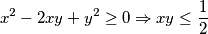 Sada nemamo kuda (ili imamo?). Iskoristimo još jednom početnu jednadžbu (tako da stvorimo odnos između
Sada nemamo kuda (ili imamo?). Iskoristimo još jednom početnu jednadžbu (tako da stvorimo odnos između 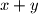 i
i 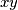 ):
): 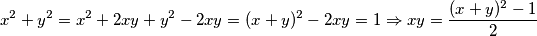 Uvrštavajući u nejednakost, dobiva se:
Uvrštavajući u nejednakost, dobiva se: 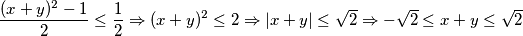 što je i trebalo dokazati.
što je i trebalo dokazati. Školjka
Školjka  i
i  realni brojevi takvi da je
realni brojevi takvi da je