Točno
17. kolovoza 2024. 15:45 (1 godina, 6 mjeseci)
Riješite jednadžbu 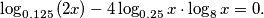
Riješite jednadžbu $$\log_{0.125}{(2x)} - 4\log_{0.25}{x} \cdot \log_{8}{x} = 0.$$
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
Prije samog rješavanja jednadžbe, napisat ćemo uvjete (domene logaritma), tj. za rješenje $x$ mora vrijediti $x>0$.\\
Svedimo sve na istu bazu, a pritom primjećujemo da je $0.125 = 2^{-3}$, $0.25 = 2^{-2}$ i $8 = 2^{3}$ odnosno da sve svodimo na bazu $2$.\\
Koristeći pravila $\log(ab) =\log a + \log b$ i $\log_{a^{b}} c = \frac{1}{b} \log_a c$, $\forall a,b,c \in \mathcal{D}_f$, jednadžba poprima oblik:
$$-\frac{1}{3}\log_{2}(2x) - 4 \left(-\frac{1}{2}\log_{2}x\right) \cdot \left(\frac{1}{3}\log_{2}x\right)=0 \Rightarrow -\frac{1}{3}\log_{2}(2x) +\frac{2}{3}\left(\log_{2}x\right) \cdot \left(\log_{2}x\right)=0$$
$$2\left(\log_{2}x\right) \cdot \left(\log_{2}x\right)-\log_{2}(2x)=0 \Rightarrow 2 \log^{2}_{2}x-\left(\log_{2}2+\log_{2}x\right) \Rightarrow 2 \log^{2}_{2}x - \log_{2}x-1=0$$
Uvedimo supstituciju $t = \log_{2}x$, pa dobijemo jednadžbu $2t^2-t-1$ čija su rješenja: $t_{1}=-\frac{1}{2}$ i $t_{2} = 2$. Vraćajući supstituciju, dobijemo da su rješenja jednadžbe:
$$\log_{2}x_{1}=t_{1} \Rightarrow x_{1} = \frac{1}{\sqrt{2}}$$
$$\log_{2}x_{2}=t_{2} \Rightarrow x_{2} = 2$$
Dakle, rješenja jednadžbe su $x\in\{\frac{1}{\sqrt{2}},2\}$.
 mora vrijediti
mora vrijediti 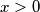 .
.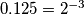 ,
, 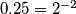 i
i  odnosno da sve svodimo na bazu
odnosno da sve svodimo na bazu  .
.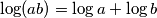 i
i 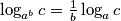 ,
, 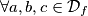 , jednadžba poprima oblik:
, jednadžba poprima oblik: 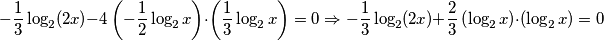
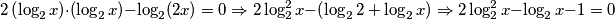 Uvedimo supstituciju
Uvedimo supstituciju 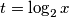 , pa dobijemo jednadžbu
, pa dobijemo jednadžbu 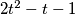 čija su rješenja:
čija su rješenja:  i
i 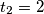 . Vraćajući supstituciju, dobijemo da su rješenja jednadžbe:
. Vraćajući supstituciju, dobijemo da su rješenja jednadžbe: 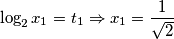
 Dakle, rješenja jednadžbe su
Dakle, rješenja jednadžbe su 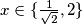 .
.  Školjka
Školjka