Točno
3. rujna 2024. 00:22 (1 godina, 5 mjeseci)
Suppose that
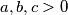
such that
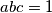
. Prove that
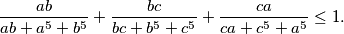
%V0
Suppose that $a, b, c > 0$ such that $abc = 1$. Prove that $$\frac{ab}{ab + a^5 + b^5} + \frac{bc}{bc + b^5 + c^5} + \frac{ca}{ca + c^5 + a^5} \leq 1.$$
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
Koristeći rearrangement inequality (ili Muirhead, kako hoćete) imamo 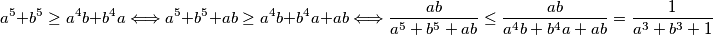
pa analogno imamo
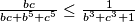
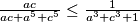
nadalje, isto koristeći rearrangemet (ili Muirhead) imamo (koristeći 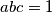 )
)
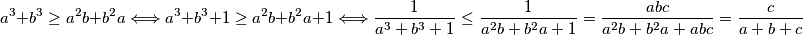
te analogno imamo
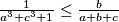
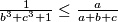
korištenjem svih prethodnih nejednakosti na kraju imamo
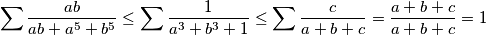
Koristeći rearrangement inequality (ili Muirhead, kako hoćete) imamo
$$a^5+b^5\ge a^4b+b^4a\Longleftrightarrow a^5+b^5+ab\ge a^4b+b^4a+ab\Longleftrightarrow \frac{ab}{a^5+b^5+ab}\le\frac{ab}{a^4b+b^4a+ab}=\frac{1}{a^3+b^3+1}$$
pa analogno imamo
$\frac{bc}{bc+b^5+c^5}\le \frac{1}{b^3+c^3+1}$
$\frac{ac}{ac+a^5+c^5}\le \frac{1}{a^3+c^3+1}$
nadalje, isto koristeći rearrangemet (ili Muirhead) imamo (koristeći $abc=1$)
$$a^3+b^3\ge a^2b+b^2a\Longleftrightarrow a^3+b^3+1\ge a^2b+b^2a+1\Longleftrightarrow \frac{1}{a^3+b^3+1}\le\frac{1}{a^2b+b^2a+1}=\frac{abc}{a^2b+b^2a+abc}=\frac{c}{a+b+c}$$
te analogno imamo
$\frac{1}{a^3+c^3+1}\le \frac{b}{a+b+c}$
$\frac{1}{b^3+c^3+1}\le \frac{a}{a+b+c}$
korištenjem svih prethodnih nejednakosti na kraju imamo
$$\sum \frac{ab}{ab+a^5+b^5}\le \sum \frac{1}{a^3+b^3+1}\le\sum\frac{c}{a+b+c}=\frac{a+b+c}{a+b+c}=1$$