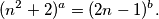Kako je 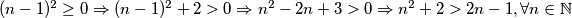 , pa je
, pa je 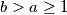
Također, ako za neki prost broj  vrijedi da
vrijedi da 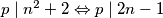 . Znači,
. Znači, 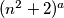 i
i 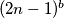 imaju zajedničke proste fakotore.
imaju zajedničke proste fakotore. 
Primijetimo da je broj 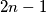 neparan, dakle onda je i
neparan, dakle onda je i 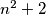 također neparan, iz čega slijedi da i
također neparan, iz čega slijedi da i  mora biti neparan.
mora biti neparan.
Imamo da je 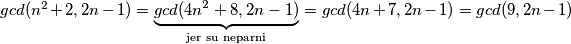 , znači
, znači 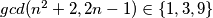 , ali kako
, ali kako  nije moguće jer
nije moguće jer 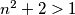 , znači ima prosti faktor, ali kako
, znači ima prosti faktor, ali kako 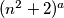 i
i 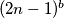 imaju zajedničke proste fakotore, onda i
imaju zajedničke proste fakotore, onda i 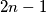 ima taj isti prosti faktor. Znači, preostaju nam mogućnosti
ima taj isti prosti faktor. Znači, preostaju nam mogućnosti 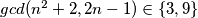 . Pretpostavimo sada da postoji prost broj
. Pretpostavimo sada da postoji prost broj 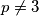 takav da
takav da 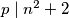 , zbog
, zbog  slijedi da
slijedi da 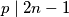 , znači kako
, znači kako  dijeli oba broja, onda dijeli i njihov najmanji zajednički dijeljitelj, znači
dijeli oba broja, onda dijeli i njihov najmanji zajednički dijeljitelj, znači 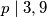 , što je kontradikcija s
, što je kontradikcija s 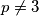 . Znači, jedini prosti faktor brojeva
. Znači, jedini prosti faktor brojeva 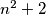 i
i 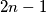 je
je  , odnosno ti brojevi su potencije broja
, odnosno ti brojevi su potencije broja  . Neka je
. Neka je 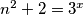 i
i 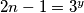 ,
, 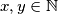 .
.
Pretpostavimo da je 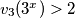 i
i 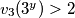 . Iz toga slijedi da
. Iz toga slijedi da 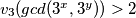 , ali
, ali 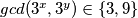 pa je
pa je 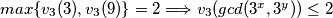 što je kontradikcija. Znači, ili
što je kontradikcija. Znači, ili 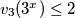 ili
ili 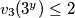 . Imamo 2 slučaja:
. Imamo 2 slučaja:
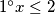

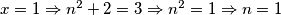 , pa imamo
, pa imamo 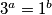 , što nema rješenja.
, što nema rješenja.

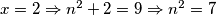 , što nema rješenja.
, što nema rješenja.
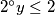

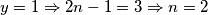 , što je kontradikcija jer je
, što je kontradikcija jer je  neparan,
neparan,

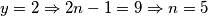 , pa imamo
, pa imamo
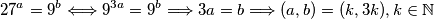
Znači jedina mogućnost je 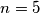 , što je rješenje zadatka.
, što je rješenje zadatka.
Kako je $(n-1)^2\ge0\Rightarrow (n-1)^2+2>0\Rightarrow n^2-2n+3>0\Rightarrow n^2+2>2n-1, \forall n\in \mathbb{N}$, pa je $b>a\ge1$
Također, ako za neki prost broj $p$ vrijedi da $p\mid n^2+2\Leftrightarrow p\mid2n-1$. Znači, $(n^2+2)^a$ i $(2n-1)^b$ imaju zajedničke proste fakotore. $(*)$
Primijetimo da je broj $2n-1$ neparan, dakle onda je i $n^2+2$ također neparan, iz čega slijedi da i $n$ mora biti neparan.
Imamo da je $gcd(n^2+2,2n-1)=\underbrace{gcd(4n^2+8,2n-1)}_{\text{jer su neparni}}=gcd(4n+7,2n-1)=gcd(9,2n-1)$, znači $gcd(n^2+2,2n-1)\in\{1,3,9\}$, ali kako $1$ nije moguće jer $n^2+2>1$, znači ima prosti faktor, ali kako $(n^2+2)^a$ i $(2n-1)^b$ imaju zajedničke proste fakotore, onda i $2n-1$ ima taj isti prosti faktor. Znači, preostaju nam mogućnosti $gcd(n^2+2, 2n-1)\in\{3,9\}$. Pretpostavimo sada da postoji prost broj $p\neq3$ takav da $p\mid n^2+2$, zbog $(*)$ slijedi da $p\mid 2n-1$, znači kako $p$ dijeli oba broja, onda dijeli i njihov najmanji zajednički dijeljitelj, znači $p\mid3,9$, što je kontradikcija s $p\neq3$. Znači, jedini prosti faktor brojeva $n^2+2$ i $2n-1$ je $3$, odnosno ti brojevi su potencije broja $3$. Neka je $n^2+2=3^x$ i $2n-1=3^y$, $x,y\in\mathbb{N}$.
Pretpostavimo da je $v_3(3^x)>2$ i $v_3(3^y)>2$. Iz toga slijedi da $v_3(gcd(3^x,3^y))>2$, ali $gcd(3^x,3^y)\in \{3,9\}$ pa je $max\{v_3(3),v_3(9)\}=2\Longrightarrow v_3(gcd(3^x,3^y))\le2$ što je kontradikcija. Znači, ili $v_3(3^x)\le2$ ili $v_3(3^y)\le2$. Imamo 2 slučaja:
$1^\circ x\le 2$
$a)$ $x=1\Rightarrow n^2+2=3\Rightarrow n^2=1\Rightarrow n=1$, pa imamo $3^a=1^b$, što nema rješenja.
$b)$ $x=2\Rightarrow n^2+2=9\Rightarrow n^2=7$, što nema rješenja.
$2^\circ y\le 2$
$a)$ $y=1\Rightarrow 2n-1=3\Rightarrow n=2$, što je kontradikcija jer je $n$ neparan,
$b)$ $y=2\Rightarrow 2n-1=9\Rightarrow n=5$, pa imamo
$$27^a=9^b\Longleftrightarrow 9^{3a}=9^b\Longrightarrow 3a=b\Longrightarrow(a,b)=(k,3k), k\in\mathbb{N}$$
Znači jedina mogućnost je $n=5$, što je rješenje zadatka.
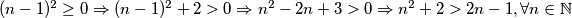 , pa je
, pa je 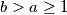
 vrijedi da
vrijedi da 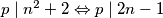 . Znači,
. Znači, 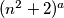 i
i 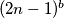 imaju zajedničke proste fakotore.
imaju zajedničke proste fakotore. 
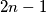 neparan, dakle onda je i
neparan, dakle onda je i 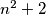 također neparan, iz čega slijedi da i
također neparan, iz čega slijedi da i  mora biti neparan.
mora biti neparan.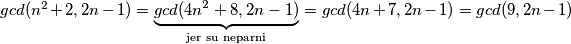 , znači
, znači 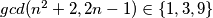 , ali kako
, ali kako  nije moguće jer
nije moguće jer 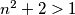 , znači ima prosti faktor, ali kako
, znači ima prosti faktor, ali kako 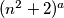 i
i 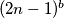 imaju zajedničke proste fakotore, onda i
imaju zajedničke proste fakotore, onda i 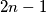 ima taj isti prosti faktor. Znači, preostaju nam mogućnosti
ima taj isti prosti faktor. Znači, preostaju nam mogućnosti 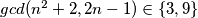 . Pretpostavimo sada da postoji prost broj
. Pretpostavimo sada da postoji prost broj 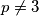 takav da
takav da 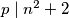 , zbog
, zbog  slijedi da
slijedi da 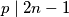 , znači kako
, znači kako  dijeli oba broja, onda dijeli i njihov najmanji zajednički dijeljitelj, znači
dijeli oba broja, onda dijeli i njihov najmanji zajednički dijeljitelj, znači 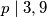 , što je kontradikcija s
, što je kontradikcija s 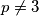 . Znači, jedini prosti faktor brojeva
. Znači, jedini prosti faktor brojeva 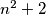 i
i 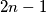 je
je  , odnosno ti brojevi su potencije broja
, odnosno ti brojevi su potencije broja  . Neka je
. Neka je 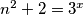 i
i 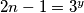 ,
, 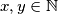 .
.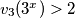 i
i 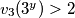 . Iz toga slijedi da
. Iz toga slijedi da 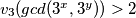 , ali
, ali 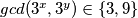 pa je
pa je 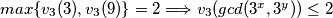 što je kontradikcija. Znači, ili
što je kontradikcija. Znači, ili 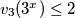 ili
ili 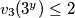 . Imamo 2 slučaja:
. Imamo 2 slučaja: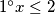

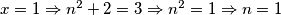 , pa imamo
, pa imamo 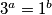 , što nema rješenja.
, što nema rješenja.
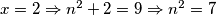 , što nema rješenja.
, što nema rješenja.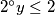

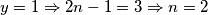 , što je kontradikcija jer je
, što je kontradikcija jer je  neparan,
neparan,
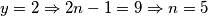 , pa imamo
, pa imamo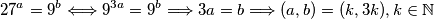
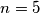 , što je rješenje zadatka.
, što je rješenje zadatka.  Školjka
Školjka  i
i  takvi da vrijedi
takvi da vrijedi