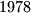 names, numbered
names, numbered 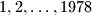 . Prove that there is at least one member whose number is the sum of the numbers of two members from his own country, or twice as large as the number of one member from his own country.
. Prove that there is at least one member whose number is the sum of the numbers of two members from his own country, or twice as large as the number of one member from his own country. Kliknite ovdje kako biste prikazali rješenje.
Pretpostavimo da tvrdnja ne vrijedi. Podijelimo skup 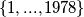 na
na  podskupa
podskupa 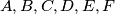 i neka su ti podskupi 'sum-free' odnosno da ne postoje dva elementa u nijednom podskupu tako da im je zbroj isto u tom podskupu. Prema Dirichletu postoji podskup s barem
i neka su ti podskupi 'sum-free' odnosno da ne postoje dva elementa u nijednom podskupu tako da im je zbroj isto u tom podskupu. Prema Dirichletu postoji podskup s barem 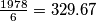 odnosno s barem
odnosno s barem 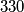 članova. BSO neka je to skup
članova. BSO neka je to skup  . Vrijedi:
. Vrijedi:
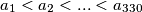 , također
, također 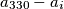 se ne nalazi u
se ne nalazi u  (zbog toga kako smo zadali
(zbog toga kako smo zadali 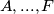 ) nego u podskupovima
) nego u podskupovima 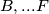 . Prema Dirichletu u podskupu
. Prema Dirichletu u podskupu  je barem
je barem 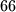 brojeva. Neka su to:
brojeva. Neka su to:
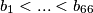 te također
te također 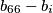 se ne nalazi u
se ne nalazi u  nego u
nego u 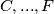 . Prema Dirichletu u
. Prema Dirichletu u  je barem
je barem  tih elemenata. Neka su to:
tih elemenata. Neka su to:
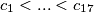 te
te 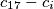 se ne nalazi u
se ne nalazi u  nego u
nego u 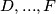 . Prema Dirichletu u
. Prema Dirichletu u  je barem
je barem  tih elemenata. Neka su to:
tih elemenata. Neka su to:
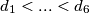 te
te 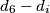 se ne nalazi u
se ne nalazi u  nego u
nego u 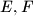 . Prema Dirichletu u
. Prema Dirichletu u  je barem
je barem  tih elemenata. Neka su to:
tih elemenata. Neka su to:
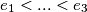 te
te 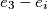 se ne nalazi u
se ne nalazi u  nego u
nego u  . U
. U  su barem dva elementa
su barem dva elementa 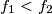 , ali
, ali 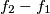 nije u
nije u  pa
pa 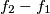 nije ni u jednom podskupu.
nije ni u jednom podskupu. 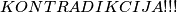
 Školjka
Školjka