Zadatak s moje 3 najdraže nejednakosti :). Dokazat ćemo sljedeću lemu:
 Za sve
Za sve 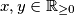 vrijedi sljedeća nejednakost
vrijedi sljedeća nejednakost ![\sqrt[3]{\frac{x}{y+7}} +\sqrt[3]{\frac{y}{x+7}}\le \sqrt[3]{\frac{x+y}{7} + 2}.](/media/m/7/5/b/75b403427f392cb3eaa70f122dc8956f.png)
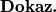 Općenito Hölderova nejednakost glasi: ako su
Općenito Hölderova nejednakost glasi: ako su 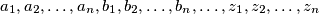 nenegativni realni brojevi i
nenegativni realni brojevi i 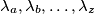 nenegativni realni brojevi sa sumom
nenegativni realni brojevi sa sumom  , onda
, onda 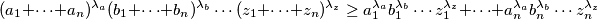 U našem slučaju, imat ćemo da je
U našem slučaju, imat ćemo da je 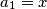 ,
, 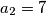 ,
, 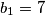 ,
, 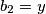 ,
, 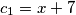 ,
, 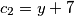 , te
, te 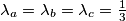 . Imamo da je
. Imamo da je
![\begin{align*}
(x+7)^{\frac{1}{3}}(7+y)^{\frac{1}{3}}\big((x+7) + (y+7)\big)^{\frac{1}{3}}
&\ge \sqrt[3]{7x(x+7)} + \sqrt[3]{7y(y+7)}\\
\Leftrightarrow \big((x+7) + (y+7)\big)^{\frac{1}{3}}
&\ge \sqrt[3]{\frac{7x}{y+7}} + \sqrt[3]{\frac{7y}{x+7}}\\
\Leftrightarrow \sqrt[3]{\frac{x+y}{7}+2}
&\ge \sqrt[3]{\frac{x}{y+7}} + \sqrt[3]{\frac{y}{x+7}}
\end{align*}](/media/m/2/0/5/20527cf47fc4d04bff6fbac9b01a8730.png)
I to dokazuje našu lemu.
Nadalje, neka je 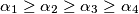 permutacija brojeva
permutacija brojeva  . Onda po rearrangementu imamo
. Onda po rearrangementu imamo
![\sqrt[3]{\frac{a}{b+7}} + \sqrt[3]{\frac{b}{c+7}} + \sqrt[3]{\frac{c}{d+7}} + \sqrt[3]{\frac{d}{a+7}} \le \sum_{i + j = 5} \sqrt[3]{\frac{\alpha_i}{\alpha_j + 7}}](/media/m/7/9/3/7938f6c17e831580a3bb3d05e1cc3e32.png)
Pa konačno po lemi imamo
![\sqrt[3]{\frac{\alpha_4}{\alpha_1+7}} +\sqrt[3]{\frac{\alpha_1}{\alpha_4+7}}\le \sqrt[3]{\frac{\alpha_4+\alpha_1}{7} + 2}](/media/m/0/e/0/0e05255079fa34c7d52bd6c5b1d62ae7.png)
![\sqrt[3]{\frac{\alpha_3}{\alpha_2+7}} +\sqrt[3]{\frac{\alpha_2}{\alpha_3+7}}\le \sqrt[3]{\frac{\alpha_3+\alpha_2}{7} + 2}](/media/m/c/b/8/cb840972d7f5e0139647b0d4770086a6.png)
Zbrajajući te dvije nejednakosti dobivamo
![\sum_{i + j = 5} \sqrt[3]{\frac{\alpha_i}{\alpha_j + 7}}\le \sqrt[3]{\frac{\alpha_4+\alpha_1}{7} + 2}+\sqrt[3]{\frac{\alpha_3+\alpha_2}{7} + 2}](/media/m/f/4/2/f42b6c46674a425c5f0e51884d5e80c2.png)
Na kraju, koristeći nejednskosti među potencijskim sredinama imamo: ![\sqrt[3]{\frac{\alpha_4+\alpha_1}{7} + 2}+\sqrt[3]{\frac{\alpha_3+\alpha_2}{7} + 2}=\sqrt[3]{\frac{\alpha_4+\alpha_1+14}{7}} + \sqrt[3]{\frac{\alpha_3+\alpha_2+14}{7}} \leqslant \sqrt[3]{4\left(\frac{\alpha_1+\alpha_2+\alpha_3+\alpha_4+28}{7}\right)} = \sqrt[3]{\frac{512}{7}}](/media/m/8/c/5/8c5766ba05a114f5387295e023a73258.png)
Znači, taj maksimum iznosi ![\sqrt[3]{\frac{512}{7}}](/media/m/c/c/1/cc108ada5175308ca63b52e4c6772476.png) , a postiže se za
, a postiže se za 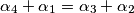 te
te 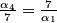 i
i 
gdje se lako dobije da se jednakost postiže za 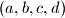 ciklička permutacija
ciklička permutacija 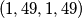 i to je to. Najssss!!!
i to je to. Najssss!!!
Zadatak s moje 3 najdraže nejednakosti :). Dokazat ćemo sljedeću lemu:
$\textbf{Lema.}$ Za sve $x,y\in \mathbb{R}_{\ge0}$ vrijedi sljedeća nejednakost
$$\sqrt[3]{\frac{x}{y+7}} +\sqrt[3]{\frac{y}{x+7}}\le \sqrt[3]{\frac{x+y}{7} + 2}.$$
$\textbf{Dokaz.}$ Općenito Hölderova nejednakost glasi: ako su $a_1, a_2, \dotsc, a_n, b_1, b_2, \dotsc, b_n, \dotsc, z_1, z_2, \dotsc, z_n$ nenegativni realni brojevi i $\lambda_a, \lambda_b, \dotsc, \lambda_z$ nenegativni realni brojevi sa sumom $1$, onda
$$(a_1 + \dotsb + a_n)^{\lambda_a} (b_1 + \dotsb + b_n)^{\lambda_b} \dotsm (z_1 + \dotsb + z_n)^{\lambda_z} \geq a_1^{\lambda_a}b_1^{\lambda_b} \dotsm z_1^{\lambda_z} + \dotsb + a_n^{\lambda_a}b_n^{\lambda_b} \dotsm z_n^{\lambda_z}$$
U našem slučaju, imat ćemo da je $a_1=x$, $a_2=7$, $b_1=7$, $b_2=y$, $c_1=x+7$, $c_2=y+7$, te $\lambda_a= \lambda_b= \lambda_c=\frac{1}{3}$. Imamo da je
\begin{align*}
(x+7)^{\frac{1}{3}}(7+y)^{\frac{1}{3}}\big((x+7) + (y+7)\big)^{\frac{1}{3}}
&\ge \sqrt[3]{7x(x+7)} + \sqrt[3]{7y(y+7)}\\
\Leftrightarrow \big((x+7) + (y+7)\big)^{\frac{1}{3}}
&\ge \sqrt[3]{\frac{7x}{y+7}} + \sqrt[3]{\frac{7y}{x+7}}\\
\Leftrightarrow \sqrt[3]{\frac{x+y}{7}+2}
&\ge \sqrt[3]{\frac{x}{y+7}} + \sqrt[3]{\frac{y}{x+7}}
\end{align*}
I to dokazuje našu lemu.
Nadalje, neka je $\alpha_1\ge\alpha_2\ge\alpha_3\ge\alpha_4$ permutacija brojeva $a,b,c,d$. Onda po rearrangementu imamo
$$ \sqrt[3]{\frac{a}{b+7}} + \sqrt[3]{\frac{b}{c+7}} + \sqrt[3]{\frac{c}{d+7}} + \sqrt[3]{\frac{d}{a+7}} \le \sum_{i + j = 5} \sqrt[3]{\frac{\alpha_i}{\alpha_j + 7}}$$
Pa konačno po lemi imamo
$$\sqrt[3]{\frac{\alpha_4}{\alpha_1+7}} +\sqrt[3]{\frac{\alpha_1}{\alpha_4+7}}\le \sqrt[3]{\frac{\alpha_4+\alpha_1}{7} + 2}$$
$$\sqrt[3]{\frac{\alpha_3}{\alpha_2+7}} +\sqrt[3]{\frac{\alpha_2}{\alpha_3+7}}\le \sqrt[3]{\frac{\alpha_3+\alpha_2}{7} + 2}$$
Zbrajajući te dvije nejednakosti dobivamo
$$\sum_{i + j = 5} \sqrt[3]{\frac{\alpha_i}{\alpha_j + 7}}\le \sqrt[3]{\frac{\alpha_4+\alpha_1}{7} + 2}+\sqrt[3]{\frac{\alpha_3+\alpha_2}{7} + 2}$$
Na kraju, koristeći nejednskosti među potencijskim sredinama imamo:
$$\sqrt[3]{\frac{\alpha_4+\alpha_1}{7} + 2}+\sqrt[3]{\frac{\alpha_3+\alpha_2}{7} + 2}=\sqrt[3]{\frac{\alpha_4+\alpha_1+14}{7}} + \sqrt[3]{\frac{\alpha_3+\alpha_2+14}{7}} \leqslant \sqrt[3]{4\left(\frac{\alpha_1+\alpha_2+\alpha_3+\alpha_4+28}{7}\right)} = \sqrt[3]{\frac{512}{7}}$$
Znači, taj maksimum iznosi $\sqrt[3]{\frac{512}{7}}$, a postiže se za $\alpha_4+\alpha_1=\alpha_3+\alpha_2$ te $\frac{\alpha_4}{7}=\frac{7}{\alpha_1}$ i $\frac{\alpha_3}{7}=\frac{7}{\alpha_2}$
gdje se lako dobije da se jednakost postiže za $(a,b,c,d)$ ciklička permutacija $(1,49,1,49)$ i to je to. Najssss!!!
 Za sve
Za sve 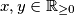 vrijedi sljedeća nejednakost
vrijedi sljedeća nejednakost ![\sqrt[3]{\frac{x}{y+7}} +\sqrt[3]{\frac{y}{x+7}}\le \sqrt[3]{\frac{x+y}{7} + 2}.](/media/m/7/5/b/75b403427f392cb3eaa70f122dc8956f.png)
 Općenito Hölderova nejednakost glasi: ako su
Općenito Hölderova nejednakost glasi: ako su 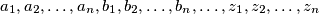 nenegativni realni brojevi i
nenegativni realni brojevi i 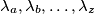 nenegativni realni brojevi sa sumom
nenegativni realni brojevi sa sumom  , onda
, onda 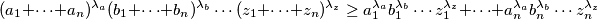 U našem slučaju, imat ćemo da je
U našem slučaju, imat ćemo da je 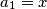 ,
, 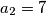 ,
, 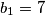 ,
, 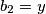 ,
, 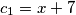 ,
, 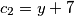 , te
, te 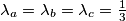 . Imamo da je
. Imamo da je![\begin{align*}
(x+7)^{\frac{1}{3}}(7+y)^{\frac{1}{3}}\big((x+7) + (y+7)\big)^{\frac{1}{3}}
&\ge \sqrt[3]{7x(x+7)} + \sqrt[3]{7y(y+7)}\\
\Leftrightarrow \big((x+7) + (y+7)\big)^{\frac{1}{3}}
&\ge \sqrt[3]{\frac{7x}{y+7}} + \sqrt[3]{\frac{7y}{x+7}}\\
\Leftrightarrow \sqrt[3]{\frac{x+y}{7}+2}
&\ge \sqrt[3]{\frac{x}{y+7}} + \sqrt[3]{\frac{y}{x+7}}
\end{align*}](/media/m/2/0/5/20527cf47fc4d04bff6fbac9b01a8730.png)
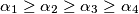 permutacija brojeva
permutacija brojeva 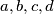 . Onda po rearrangementu imamo
. Onda po rearrangementu imamo![\sqrt[3]{\frac{a}{b+7}} + \sqrt[3]{\frac{b}{c+7}} + \sqrt[3]{\frac{c}{d+7}} + \sqrt[3]{\frac{d}{a+7}} \le \sum_{i + j = 5} \sqrt[3]{\frac{\alpha_i}{\alpha_j + 7}}](/media/m/7/9/3/7938f6c17e831580a3bb3d05e1cc3e32.png)
![\sqrt[3]{\frac{\alpha_4}{\alpha_1+7}} +\sqrt[3]{\frac{\alpha_1}{\alpha_4+7}}\le \sqrt[3]{\frac{\alpha_4+\alpha_1}{7} + 2}](/media/m/0/e/0/0e05255079fa34c7d52bd6c5b1d62ae7.png)
![\sqrt[3]{\frac{\alpha_3}{\alpha_2+7}} +\sqrt[3]{\frac{\alpha_2}{\alpha_3+7}}\le \sqrt[3]{\frac{\alpha_3+\alpha_2}{7} + 2}](/media/m/c/b/8/cb840972d7f5e0139647b0d4770086a6.png)
![\sum_{i + j = 5} \sqrt[3]{\frac{\alpha_i}{\alpha_j + 7}}\le \sqrt[3]{\frac{\alpha_4+\alpha_1}{7} + 2}+\sqrt[3]{\frac{\alpha_3+\alpha_2}{7} + 2}](/media/m/f/4/2/f42b6c46674a425c5f0e51884d5e80c2.png)
![\sqrt[3]{\frac{\alpha_4+\alpha_1}{7} + 2}+\sqrt[3]{\frac{\alpha_3+\alpha_2}{7} + 2}=\sqrt[3]{\frac{\alpha_4+\alpha_1+14}{7}} + \sqrt[3]{\frac{\alpha_3+\alpha_2+14}{7}} \leqslant \sqrt[3]{4\left(\frac{\alpha_1+\alpha_2+\alpha_3+\alpha_4+28}{7}\right)} = \sqrt[3]{\frac{512}{7}}](/media/m/8/c/5/8c5766ba05a114f5387295e023a73258.png)
![\sqrt[3]{\frac{512}{7}}](/media/m/c/c/1/cc108ada5175308ca63b52e4c6772476.png) , a postiže se za
, a postiže se za 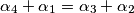 te
te 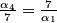 i
i 
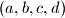 ciklička permutacija
ciklička permutacija 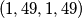 i to je to. Najssss!!!
i to je to. Najssss!!!  Školjka
Školjka ![S = \sqrt[3]{\frac{a}{b+7}} + \sqrt[3]{\frac{b}{c+7}} + \sqrt[3]{\frac{c}{d+7}} + \sqrt[3]{\frac{d}{a+7}},](/media/m/f/6/5/f65475dcb0df99b384f915c2001a7ee1.png) where
where  ,
,  ,
,  ,
,  are nonnegative real numbers which satisfy
are nonnegative real numbers which satisfy 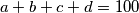 .
.