Točno
4. rujna 2024. 21:55 (1 godina, 5 mjeseci)
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
Kliknite ovdje kako biste prikazali rješenje.
Vrlo kratko riješenje:)
Neka je s 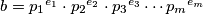 , odnosno
, odnosno 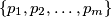 je skup prostih dijeljitelja broja
je skup prostih dijeljitelja broja  , znamo da postoje jer
, znamo da postoje jer 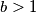 . Tada odaberimo bilo koji
. Tada odaberimo bilo koji 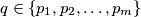 te označimo s
te označimo s 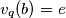 , najveću potenciju broja
, najveću potenciju broja  koja dijeli
koja dijeli  . Neka je
. Neka je 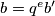 . Uzmemo
. Uzmemo 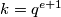 , pa imamo
, pa imamo 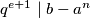 , ali ako
, ali ako 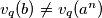 slijedi da je
slijedi da je 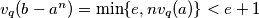 što je kontradikcija jer iz
što je kontradikcija jer iz 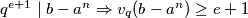 . Znači
. Znači 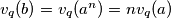 iz čega slijedi da
iz čega slijedi da 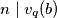 , tj.
, tj. 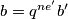 za sve
za sve 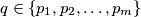 , tj imamo da je
, tj imamo da je
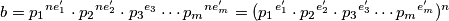
pa je 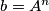 za neki
za neki  i to je to. Najssss!
i to je to. Najssss!
 Školjka
Školjka 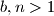 be integers. Suppose that for each
be integers. Suppose that for each  there exists an integer
there exists an integer 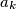 such that
such that 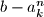 is divisible by
is divisible by 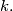 Prove that
Prove that 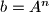 for some integer
for some integer