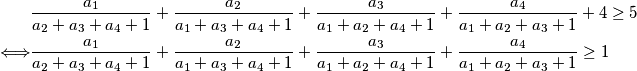Točno
6. rujna 2024. 23:29 (1 godina, 4 mjeseci)
Neka su $a_1$, $a_2$, $a_3$ i $a_4$ pozitivni realni brojevi takvi da je $a_1a_2a_3a_4 = 1$. Dokaži da je
\[ \frac{a_1}{a_2 + a_3 + a_4 + 1} + \frac{a_2}{a_1 + a_3 + a_4 + 1} + \frac{a_3}{a_1 + a_2 + a_4 + 1} + \frac{a_4}{a_1 + a_2 + a_3 + 1}
\geq 1 \text{.} \]
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
Neka je 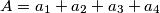 , pa koristeći
, pa koristeći 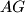 nejednakost imamo
nejednakost imamo
![A=a_1+a_2+a_3+a_4\ge 4\sqrt[4]{ a_1a_2a_3a_4}=4](/media/m/4/5/d/45dc38796085bae8abb504ee8a326333.png)
Iz toga slijedi
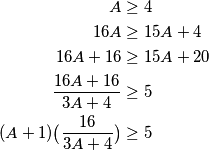 Nadalje, koristeći
Nadalje, koristeći 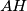 nejednakost imamo
nejednakost imamo 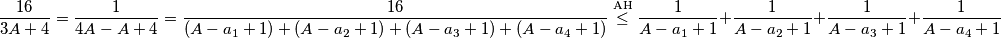 Pa imamo
Pa imamo
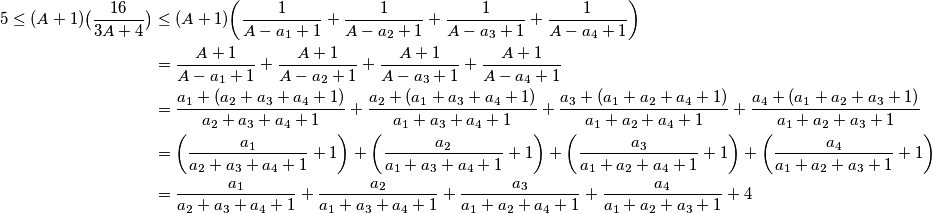 Iz čega direktno slijedi tražena nejednakost;
Iz čega direktno slijedi tražena nejednakost;
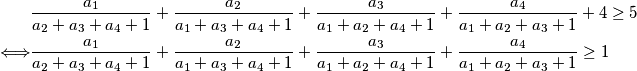
Čime smo dokazali traženu nejednakost i to je to. Najsss!
Neka je $A=a_1+a_2+a_3+a_4$, pa koristeći $AG$ nejednakost imamo
$$A=a_1+a_2+a_3+a_4\ge 4\sqrt[4]{ a_1a_2a_3a_4}=4$$
Iz toga slijedi
\begin{align*}
A&\ge4 \\
16A&\ge 15A+4\\
16A+16&\ge 15A+20\\
\frac{16A+16}{3A+4}&\ge5\\
(A+1)\big(\frac{16}{3A+4}\big)&\ge5
\end{align*}
Nadalje, koristeći $AH$ nejednakost imamo
$$\frac{16}{3A+4}=\frac{1}{4A-A+4}=\frac{16}{(A-a_1+1)+(A-a_2+1)+(A-a_3+1)+(A-a_4+1)}\stackrel{\text{AH}}{\le}\frac{1}{A-a_1+1} + \frac{1}{A-a_2+1} + \frac{1}{A-a_3+1} + \frac{1}{A-a_4+1}$$
Pa imamo
\begin{align*}
5\le(A+1)\big(\frac{16}{3A+4}\big)&\le(A+1)\bigg(\frac{1}{A-a_1+1} + \frac{1}{A-a_2+1} + \frac{1}{A-a_3+1} + \frac{1}{A-a_4+1}\bigg)\\
&=\frac{A+1}{A-a_1+1} + \frac{A+1}{A-a_2+1} + \frac{A+1}{A-a_3+1} + \frac{A+1}{A-a_4+1}\\
&=\frac{a_1+(a_2+a_3+a_4+1)}{a_2 + a_3 + a_4 + 1} + \frac{a_2+(a_1+a_3+a_4+1)}{a_1 + a_3 + a_4 + 1} + \frac{a_3+(a_1+a_2+a_4+1)}{a_1 + a_2 + a_4 + 1} + \frac{a_4+(a_1+a_2+a_3+1)}{a_1 + a_2 + a_3 + 1}\\
&=\bigg(\frac{a_1}{a_2 + a_3 + a_4 + 1}+1\bigg) + \bigg(\frac{a_2}{a_1 + a_3 + a_4 + 1}+1\bigg) + \bigg(\frac{a_3}{a_1 + a_2 + a_4 + 1} +1\bigg)+ \bigg(\frac{a_4}{a_1 + a_2 + a_3 + 1}+1\bigg)\\
&=\frac{a_1}{a_2 + a_3 + a_4 + 1} + \frac{a_2}{a_1 + a_3 + a_4 + 1} + \frac{a_3}{a_1 + a_2 + a_4 + 1} + \frac{a_4}{a_1 + a_2 + a_3 + 1}+4
\end{align*}
Iz čega direktno slijedi tražena nejednakost;
\begin{align*}
&\frac{a_1}{a_2 + a_3 + a_4 + 1} + \frac{a_2}{a_1 + a_3 + a_4 + 1} + \frac{a_3}{a_1 + a_2 + a_4 + 1} + \frac{a_4}{a_1 + a_2 + a_3 + 1}+4\ge5\\
\Longleftrightarrow &\frac{a_1}{a_2 + a_3 + a_4 + 1} + \frac{a_2}{a_1 + a_3 + a_4 + 1} + \frac{a_3}{a_1 + a_2 + a_4 + 1} + \frac{a_4}{a_1 + a_2 + a_3 + 1}\ge 1
\end{align*}
Čime smo dokazali traženu nejednakost i to je to. Najsss!
| 11. rujna 2024. 19:55 | Patrlk | Točno |
 Školjka
Školjka  ,
,  ,
, 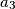 i
i 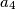 pozitivni realni brojevi takvi da je
pozitivni realni brojevi takvi da je 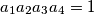 . Dokaži da je
. Dokaži da je 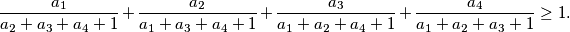
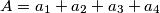 , pa koristeći
, pa koristeći 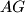 nejednakost imamo
nejednakost imamo![A=a_1+a_2+a_3+a_4\ge 4\sqrt[4]{ a_1a_2a_3a_4}=4](/media/m/4/5/d/45dc38796085bae8abb504ee8a326333.png)
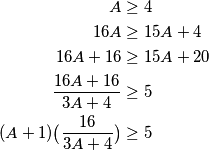 Nadalje, koristeći
Nadalje, koristeći 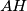 nejednakost imamo
nejednakost imamo 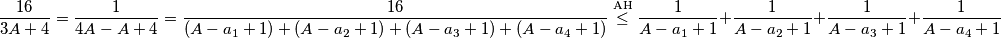 Pa imamo
Pa imamo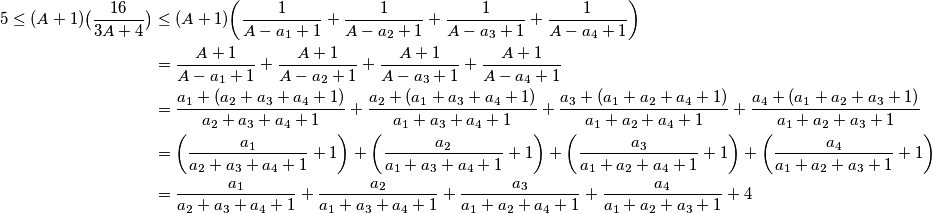 Iz čega direktno slijedi tražena nejednakost;
Iz čega direktno slijedi tražena nejednakost;