Determine that all such that the numbers and have no common divisor.
%V0
Determine that all $k \in \mathbb{Z}$ such that $\forall n$ the numbers $4n+1$ and $kn+1$ have no common divisor.
Warning: You haven't solved this problem yet. Click here to display the solution.
Pogledat ćemo sljedeća slučaja:
Ako je 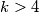, tada vrijedi
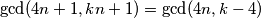
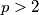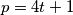ako je prost broj takav da i , tada možemo uzeti 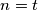, a ako je 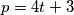, tada je 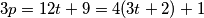, odnosno 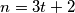. Dakle, .
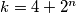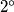Ako je , tada su jedina rješenja u skupu 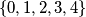, što se lako provjeri da rade samo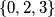
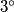Ako je , neka je 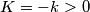, pa je
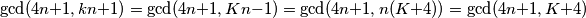
, pa je 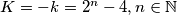, i to je to. Najsss!
Pogledat ćemo sljedeća $3$ slučaja:
$1^{\circ}$ Ako je $ k > 4$, tada vrijedi
$$ \gcd(4n + 1, kn + 1) = \gcd(4n, k - 4)$$
ako je $ p > 2$ prost broj takav da $ p \mid k - 4$ i $ p = 4t + 1$, tada možemo uzeti $ n = t$, a ako je $ p = 4t + 3$, tada je $ 3p = 12t + 9 = 4(3t + 2) + 1$, odnosno $n=3t+2$. Dakle, $ k = 4 + 2^n$.
$2^{\circ}$ Ako je $ 0 \le k \le 4$, tada su jedina rješenja u skupu $ \{0, 1 ,2 , 3 ,4\}$, što se lako provjeri da rade samo $\{0,2,3\}$
$3^{\circ}$ Ako je $ k < 0$, neka je $ K = -k > 0$, pa je
$$\gcd(4n + 1, kn + 1) = \gcd(4n + 1, Kn - 1) = \gcd(4n + 1, n(K + 4)) = \gcd(4n + 1, K + 4)$$
, pa je $ K = -k = 2^n -4, n \in \mathbb{N}$, i to je to. Najsss!
Školjka 
such that 
the numbers 
and 
have no common divisor. 
slučaja:
Ako je 
, tada vrijedi
prost broj takav da 
i 
, tada možemo uzeti 
, a ako je 
, tada je 
, odnosno 
. Dakle, 
.
Ako je 
, tada su jedina rješenja u skupu 
, što se lako provjeri da rade samo 
Ako je 
, neka je 
, pa je
, i to je to. Najsss!