Točno
17. rujna 2024. 12:45 (1 godina, 5 mjeseci)
Korisnik: ceva18
Zadatak: Školsko/gradsko natjecanje iz matematike 2015, SŠ2 A 1 (Sakrij tekst zadatka)
Zadatak: Školsko/gradsko natjecanje iz matematike 2015, SŠ2 A 1 (Sakrij tekst zadatka)
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
Kliknite ovdje kako biste prikazali rješenje.
Neka je 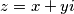 , gdje je
, gdje je 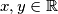 . Cilj nam je srediti izraz
. Cilj nam je srediti izraz 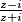 tako da vidimo koji je njegov realni dio. Slijedi:
tako da vidimo koji je njegov realni dio. Slijedi: ![\frac{z-i}{z+i}=\frac{x+yi-i}{x+yi+i} = \frac{x+i\left(y-1\right)}{x+i\left(y+1\right)} \cdot \underbrace{\frac{x-i\left(y+1\right)}{x-i\left(y+1\right)}}_{=1}= \frac{\left[x+i\left(y-1\right)\right]\left[x-i\left(y+1\right)\right]}{\left[x+i\left(y+1\right)\right]\left[x-i\left(y+1\right)\right]} = \frac{x^{2}+ix\left(y-1\right)-ix\left(y+1\right)-i^{2}(y+1)(y-1)}{x^{2}-\left(i(y+1)\right)^{2}}](/media/m/9/2/7/9278922294eac42cc880d33e17b174da.png)
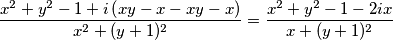 Dakle,
Dakle, 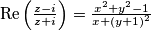 . Iz pretpostavke da je realni dio jednak nuli, slijedi:
. Iz pretpostavke da je realni dio jednak nuli, slijedi: 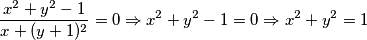 Što trebamo dobiti? Moramo dobiti da je
Što trebamo dobiti? Moramo dobiti da je 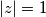 , a znamo da je
, a znamo da je 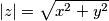 . Korjenovanjem jednadžbe, dobijemo:
. Korjenovanjem jednadžbe, dobijemo: 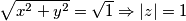 , što je i trebalo dokazati.
, što je i trebalo dokazati.
Međutim, pripazimo da tvrdnja ne vrijedi 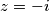 jer za taj
jer za taj  nije definiran razlomak
nije definiran razlomak 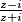 , a onda nije ni
, a onda nije ni 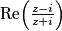 definiran. Prema tome, taj uvjet nema smisla promatrati.
definiran. Prema tome, taj uvjet nema smisla promatrati.
 Školjka
Školjka 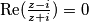 , onda je
, onda je 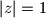 .
.