Točno
24. rujna 2024. 22:40 (1 godina, 5 mjeseci)
Neka su

pozitivni realni brojevi takvi da vrijedi
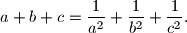
Dokaži
![2(a + b + c) \geq \sqrt[3]{7a^2b + 1} + \sqrt[3]{7b^2c + 1} + \sqrt[3]{7c^2a + 1} \text{.}](/media/m/b/d/5/bd5f82834e8a41edd87111ad765bc5c5.png)
Nađi sve trojke
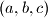
za koje vrijedi jednakost.
%V0
Neka su $a, b, c$ pozitivni realni brojevi takvi da vrijedi $$
a + b + c = \frac{1}{a^2} + \frac{1}{b^2} + \frac{1}{c^2} \text{.}
$$ Dokaži $$
2(a + b + c) \geq \sqrt[3]{7a^2b + 1} + \sqrt[3]{7b^2c + 1} + \sqrt[3]{7c^2a + 1} \text{.}
$$ Nađi sve trojke $(a, b, c)$ za koje vrijedi jednakost.
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
Primijetimo da
Dakle, po Hölderu imamo:
Primijetimo da \begin{center}
$8(a+b+c)=\sum_{}\frac{1}{a^2}+7b=\sum_{}\frac{7a^2b+1}{a^2}$\\
\end{center}
Dakle, po Hölderu imamo:\begin{center}
$(2(a+b+c))^3=\sum_{}\frac{7a^2b+1}{a^2}(a+b+c)(a+b+c) \geq (\sum_{}\sqrt[3]{7a^2b+1})^3$\\\\
$\Leftrightarrow (2(a+b+c))^3 \geq (\sum_{}\sqrt[3]{7a^2b+1})^3$\\\\
$\Leftrightarrow 2(a+b+c) \geq \sqrt[3]{7a^2b+1}+\sqrt[3]{7b^2c+1}+\sqrt[3]{7c^2a+1}$
\end{center}
| 24. rujna 2024. 23:47 | loki6 | Točno |