Točno
25. rujna 2024. 19:08 (1 godina, 5 mjeseci)
Za pozitivne realne brojeve

,

takve da vrijedi

dokaži:

%V0
Za pozitivne realne brojeve $a_1, a_2, ..., a_n$, $n \geq 2$ takve da vrijedi $a_1 + a_2 + ... + a_n \leq 1$ dokaži:
$$a_1+a_2+...+a_n + \frac{1}{a_1} +\frac{1}{a_2} + ... +\frac{1}{a_n} \geq n^2 + \frac{1}{a_1+a_2+...+a_n}$$
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
Primijenjujući $AH$ nejednakost dobivamo
$$\frac{1}{a_2} + ... +\frac{1}{a_n}\ge \frac{n^2}{a_1+a_2+\cdots+a_n}$$
Sada, neka je $\sum a_i=x$, te iz uvjeta zadatka imamo $x\le 1$.
Iz iskorištene $AH$ nejednakosti te uvedene oznake vidimo da je dovoljno dokazati
$$x+\frac{n^2}{x}\ge n^2+\frac{1}{x}$$
Množeći obje strane nejednakosti s $x>0$ dobivamo ekvivalentnu nejednakost.
\begin{align*}
x^2+n^2&\ge n^2x+1\\
n^2-n^2x&\ge 1-x^2\\
n^2(1-x)&\ge(1-x)(1+x)\\
n^2&\ge1+x &(*)
\end{align*}
što očito vrijedi jer $1+x\le 2\implies n^2 \ge2^2=4>2\ge 1+x$
Sada, promotrimo još malo $(*)$. Naravno, djelili smo s $1-x$, ali u slučaju da $x=1$, jasno vidimo da onda u početnoj nejednakosti uvijek vrijedi jednakost;
$$1+n^2=n^2+1$$
Sve u svemu imamo
$$a_1+a_2+...+a_n + \frac{1}{a_1} +\frac{1}{a_2} + ... +\frac{1}{a_n}\ge a_1+a_2+...+a_n+\frac{n^2}{a_1+a_2+\cdots+a_n} \ge n^2 + \frac{1}{a_1+a_2+...+a_n}$$
Tako da smo nejednakost dokazali $\forall x\le1,n\ge2$. \\
Vidimo da je u $(*)$ nejednakost uvijek stroga za $x\neq1$, znači jednakost se postiže ako i samo ako $x=1$ i $a_1=a_2=\ldots=a_n$ zbog jednakosti u $AH$, odnosno $a_1=a_2=\ldots=a_n=\frac{1}{n}$.
| 25. rujna 2024. 18:01 | msaric | Točno |
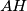 nejednakost dobivamo
nejednakost dobivamo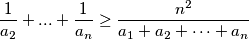 Sada, neka je
Sada, neka je 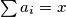 , te iz uvjeta zadatka imamo
, te iz uvjeta zadatka imamo 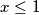 . Iz iskorištene
. Iz iskorištene 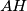 nejednakosti te uvedene oznake vidimo da je dovoljno dokazati
nejednakosti te uvedene oznake vidimo da je dovoljno dokazati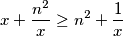
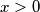 dobivamo ekvivalentnu nejednakost.
dobivamo ekvivalentnu nejednakost. 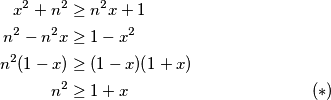 što očito vrijedi jer
što očito vrijedi jer 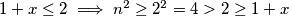
 . Naravno, djelili smo s
. Naravno, djelili smo s  , ali u slučaju da
, ali u slučaju da  , jasno vidimo da onda u početnoj nejednakosti uvijek vrijedi jednakost;
, jasno vidimo da onda u početnoj nejednakosti uvijek vrijedi jednakost;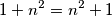
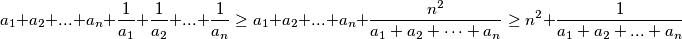 Tako da smo nejednakost dokazali
Tako da smo nejednakost dokazali 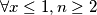 .
.  nejednakost uvijek stroga za
nejednakost uvijek stroga za 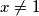 , znači jednakost se postiže ako i samo ako
, znači jednakost se postiže ako i samo ako  i
i 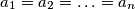 zbog jednakosti u
zbog jednakosti u 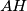 , odnosno
, odnosno 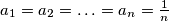 .
.  Školjka
Školjka  ,
,  takve da vrijedi
takve da vrijedi  dokaži:
dokaži: 