Točno
28. rujna 2024. 21:48 (1 godina, 4 mjeseci)
Let 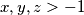 . Prove that
. Prove that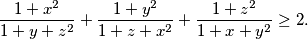
Let $x, y, z > -1$. Prove that\[\frac{1+x^2}{1+y+z^2} + \frac{1+y^2}{1+z+x^2} + \frac{1+z^2}{1+x+y^2} \geq 2.\]
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
Primijetimo da su svi brojnici $1+x^2,1+y^2,1+z^2$ očito pozitivni, te za svaki nazivnik vrijedi $a>-1 \implies 1+a+b^2>0$ za sve $(a,b)\in\{(x,y),(y,z),(z,x)\}$. Nadalje, iz trivijalne nejednakosti $(x-1)^2\ge0\implies x\le\frac{x^2+1}{2}$.\\
Analogno dobivamo $y\le\frac{y^2+1}{2}, z\le\frac{z^2+1}{2}$.\\
Iz tih nejednakosti dobivamo
$$\sum\frac{1 + x ^ 2}{1 + y + z ^ 2}\geq \sum \frac {1 + x ^ 2}{1+ \frac {y ^ 2 + 1}{2} + z ^ 2}= \sum\frac {2(1 + x ^ 2)}{y ^ 2 + 2z ^ 2 + 3} = \sum \frac {2(1 + x ^ 2)}{(y ^ 2 + 1) + 2(z ^ 2 + 1)}$$
Sada, neka je $a=x^2+1,b=y^2+1,c=z^2+1$
Potrebno je dokazati $\sum \frac{a}{b+2c}\ge1$
Primijetimo da je
$$\sum \frac{a}{b+2c}=\sum \frac{a}{b+2c}\cdot \frac{\sum a(b+2c)}{\sum a(b+2c)}=\frac{ \sum\frac{a}{b+2c}\cdot\sum a(b+2c)}{\sum a(b+2c)}$$
Pa po $CSB$ nejednakosti imamo
$$\sum\frac{a}{b+2c}\cdot\sum a(b+2c)\ge(\sum a)^2\implies\frac{ \sum\frac{a}{b+2c}\cdot\sum a(b+2c)}{\sum a(b+2c)}\ge\frac{(\sum a)^2}{\sum a(b+2c)}=\frac{(\sum a)^2}{3\sum ab}$$
S obzirom da $\sum a^2\ge \sum ab\implies (\sum a)^2\ge3\sum ab\implies \frac{(\sum a)^2}{3\sum ab}\ge 1$, iz čega konačno imamo
\begin{align*}
\sum \frac{1 + x^2}{1 + y + z^2} &\geq \sum \frac{2(1 + x^2)}{(y^2 + 1) + 2(z^2 + 1)}\\
&= 2 \sum \frac{1 + x^2}{y^2 + 1 + 2(z^2 + 1)}\\
&= 2 \sum \frac{a}{b + 2c} \geq 2 \cdot 1 = 2
\end{align*}
I to je to. Najsss!
| 26. rujna 2024. 11:06 | Froon | Točno |
 očito pozitivni, te za svaki nazivnik vrijedi
očito pozitivni, te za svaki nazivnik vrijedi 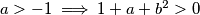 za sve
za sve 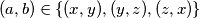 . Nadalje, iz trivijalne nejednakosti
. Nadalje, iz trivijalne nejednakosti  .
.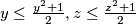 .
.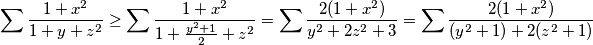
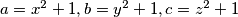

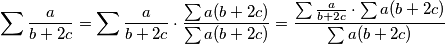
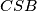 nejednakosti imamo
nejednakosti imamo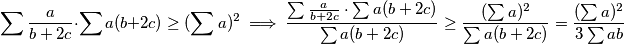 S obzirom da
S obzirom da 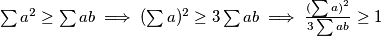 , iz čega konačno imamo
, iz čega konačno imamo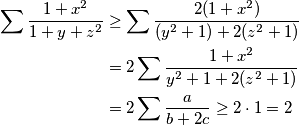
 Školjka
Školjka  . Prove that
. Prove that