Točno
28. listopada 2024. 12:36 (1 godina, 3 mjeseci)
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
Kliknite ovdje kako biste prikazali rješenje.
Uvjet zadatka je da su svi relativno prosti brojevi s  koji su manji od
koji su manji od  članovi aritmetičkog niza. Očito
članovi aritmetičkog niza. Očito 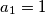 i
i 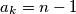 .
.
Neka je 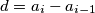 . Za
. Za 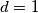 dobivamo da su svi brojevi koji su manji od
dobivamo da su svi brojevi koji su manji od  relativno prosti s
relativno prosti s  , pa je
, pa je  prost broj.
prost broj.
Za 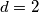 dobivamo da su članovi niza redom
dobivamo da su članovi niza redom 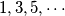 pa
pa  mora biti potencija broja
mora biti potencija broja  .
.
Pretpostavimo sad da je 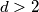 . Promotrimo
. Promotrimo 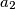 . Kako je on prvi član niza nakon
. Kako je on prvi član niza nakon  , on mora biti prost. Zapišimo
, on mora biti prost. Zapišimo 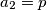 , tada
, tada 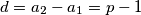 .
.
Po formuli za članove aritmetičkog niza imamo:
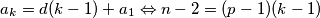
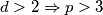 pa
pa 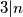 , odnosno
, odnosno 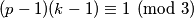 . To znači da
. To znači da 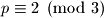 , ali tad
, ali tad
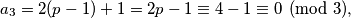
što je kontradikcija jer su 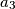 i
i  relativno prosti.
relativno prosti.
Dakle,  mora biti prost ili potencija broja
mora biti prost ili potencija broja  .
.
 Školjka
Školjka 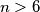 be an integer and
be an integer and 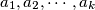 be all the natural numbers less than
be all the natural numbers less than 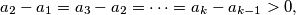
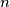 must be either a prime number or a power of
must be either a prime number or a power of 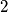 .
.