Točno
13. studenoga 2013. 19:57 (10 godine, 5 mjeseci)
Sakrij rješenje
Dokažite da je
.
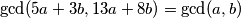
%V0
Dokažite da je $\gcd(5a+3b,13a+8b)=\gcd(a,b)$.
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
%V0
$gcd(5a+3b,13a+8b)=gdc(13a+8b,5a+3b) \\ =gcd(13a+8b-(5a+3b),5a+3b) \\ =gcd(8a+5b,5a+3b) \\=gcd(8a+5b-(5a+3b),5a+3b)\\=gcd(3a+2b,5a+3b)\\=gcd(5a+3b,3a+2b)\\=gcd(2a+b,3a+2b)\\=gcd(2a+b,a+b)\\=gcd(a,a+b)\\=gcd(a,b)$
| 16. studenoga 2013. 22:24 | grga | Točno |
Školjka 