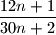
Dokaži da je razlomak neskrativ za sve prirodne brojeve .
%V0
Dokaži da je razlomak $\dfrac{12n+1}{30n+2}$ neskrativ za sve prirodne brojeve $n$.
Upozorenje: Ovaj zadatak još niste riješili! Kliknite ovdje kako biste prikazali rješenje.
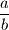
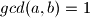
Da bi razlomak bio neskrativ mora vrjediti . Dakle treba dokazati da
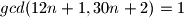
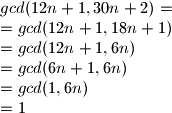
%V0
Da bi razlomak $\dfrac{a}{b}$ bio neskrativ mora vrjediti $gcd(a,b)=1$. Dakle treba dokazati da $gcd(12n+1,30n+2)=1$
$gcd(12n+1,30n+2)=\\=gcd(12n+1,18n+1)\\=gcd(12n+1,6n)\\=gcd(6n+1,6n)\\=gcd(1,6n)\\=1$
Školjka 
neskrativ za sve prirodne brojeve 
. 
bio neskrativ mora vrjediti 
. Dakle treba dokazati da 
