Školjka

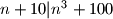
%V0 Ako $a|b$ onda $gcd(a,b)=a$ $gcd(n+10,n^3+100)=n+10$ U ovom izrazu nam je tesko ista zakljuciti radi clana $n^3$, pa pokusajmo se njega rjesiti. $gcd(n+10,n^3 + 100 - n^2(n+10) )=n+10$ $gcd(n+10,100-10n^2)=n+10$ Ovaj zraz je nsto bolji, no pokusajmo se rjesiti i $10n^2$ $gcd(n+10,100-10n^2+10n(n+10))=n+10$ $gcd(n+10,100+10n)=n+10$ $gcd(n+10,10n+100 - 10(n+10))=n+10$ $gcd(n+10,-900)=n+10$ $gcd(n+10,900)=n+10$ Dakle, $n+10|900$. Najveci djeljitelj od $900$ je on sam, pa je $n+10=900$ to jest $n=890$