Točno
13. studenoga 2013. 20:23 (12 godine, 4 mjeseci)
Sakrij rješenje
Sakrij rješenje
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
Kliknite ovdje kako biste prikazali rješenje.
Nuzno je i dovoljno pokazati da je 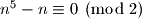 ,
, 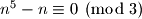 i
i 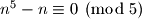 .
.
Promatrajmo ostatke koje pete potencije daju pri djelnjenju s u ovisnosti o brojevima
u ovisnosti o brojevima
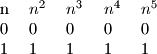
Primjetimo da su stupci i
i 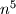 potpuno isti. Dakle znamo da uvjek vrijedi
potpuno isti. Dakle znamo da uvjek vrijedi 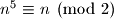 to jest
to jest 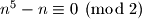
Promatrajmo ostatke koje pete potencije daju pri djelnjenju s u ovisnosti o brojevima
u ovisnosti o brojevima
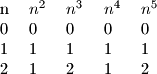
Primjetimo da su stupci i
i 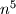 potpuno isti. Dakle znamo da uvjek vrijedi
potpuno isti. Dakle znamo da uvjek vrijedi 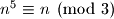 to jest
to jest 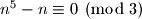
Promatrajmo ostatke koje pete potencije daju pri djelnjenju s u ovisnosti o brojevima
u ovisnosti o brojevima
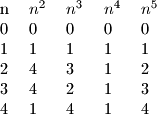
Primjetimo da su stupci i
i 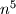 potpuno isti. Dakle znamo da uvjek vrijedi
potpuno isti. Dakle znamo da uvjek vrijedi 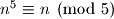 to jest
to jest 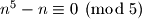
Dakle, kako je izraz uvjek djeljiv s
 i
i  , uvjek je djeljiv s
, uvjek je djeljiv s  .
.
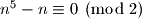 ,
, 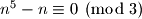 i
i 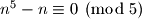 .
. Promatrajmo ostatke koje pete potencije daju pri djelnjenju s
 u ovisnosti o brojevima
u ovisnosti o brojevima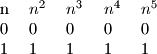
Primjetimo da su stupci
 i
i 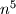 potpuno isti. Dakle znamo da uvjek vrijedi
potpuno isti. Dakle znamo da uvjek vrijedi 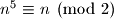 to jest
to jest 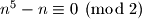
Promatrajmo ostatke koje pete potencije daju pri djelnjenju s
 u ovisnosti o brojevima
u ovisnosti o brojevima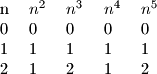
Primjetimo da su stupci
 i
i 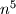 potpuno isti. Dakle znamo da uvjek vrijedi
potpuno isti. Dakle znamo da uvjek vrijedi 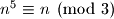 to jest
to jest 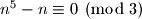
Promatrajmo ostatke koje pete potencije daju pri djelnjenju s
 u ovisnosti o brojevima
u ovisnosti o brojevima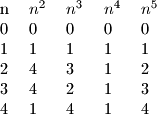
Primjetimo da su stupci
 i
i 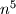 potpuno isti. Dakle znamo da uvjek vrijedi
potpuno isti. Dakle znamo da uvjek vrijedi 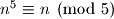 to jest
to jest 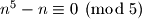
Dakle, kako je izraz uvjek djeljiv s

 i
i  , uvjek je djeljiv s
, uvjek je djeljiv s  .
.  Školjka
Školjka 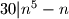 .
.