Točno
13. studenoga 2013. 20:27 (12 godine, 4 mjeseci)
Sakrij rješenje
Sakrij rješenje
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
Kliknite ovdje kako biste prikazali rješenje.
Potrebno je odrediti za koje  vrijedi
vrijedi 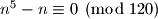 sto je ekvivalentno tome da odredimo za koje
sto je ekvivalentno tome da odredimo za koje 
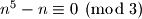 ,
, 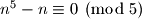 i
i 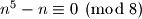 .
.
Promatrajmo ostatke koje pete potencije daju pri djelnjenju s u ovisnosti o brojevima
u ovisnosti o brojevima
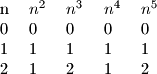
Primjetimo da su stupci i
i 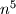 potpuno isti. Dakle znamo da uvjek vrijedi
potpuno isti. Dakle znamo da uvjek vrijedi 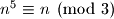 to jest
to jest 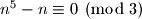
Promatrajmo ostatke koje pete potencije daju pri djelnjenju s u ovisnosti o brojevima
u ovisnosti o brojevima
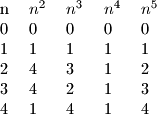
Primjetimo da su stupci i
i 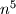 potpuno isti. Dakle znamo da uvjek vrijedi
potpuno isti. Dakle znamo da uvjek vrijedi 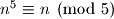 to jest
to jest 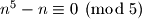
Potrebno je dakle jos provjeriti za koje vrijedi
vrijedi 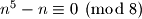
Promatrajmo ostatke koje pete potencije daju pri djelnjenju s u ovisnosti o brojevima
u ovisnosti o brojevima
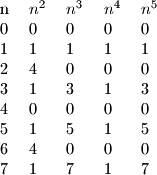
Dakle,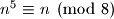 ako i samo ako je
ako i samo ako je 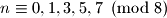 . Dakle,
. Dakle, 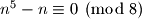 vrijedi za sve
vrijedi za sve  koji su djeljivi s
koji su djeljivi s  ili su neparni.
ili su neparni.
 vrijedi
vrijedi 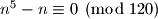 sto je ekvivalentno tome da odredimo za koje
sto je ekvivalentno tome da odredimo za koje 
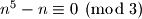 ,
, 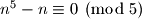 i
i 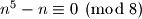 .
.Promatrajmo ostatke koje pete potencije daju pri djelnjenju s
 u ovisnosti o brojevima
u ovisnosti o brojevima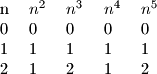
Primjetimo da su stupci
 i
i 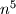 potpuno isti. Dakle znamo da uvjek vrijedi
potpuno isti. Dakle znamo da uvjek vrijedi 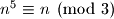 to jest
to jest 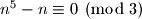
Promatrajmo ostatke koje pete potencije daju pri djelnjenju s
 u ovisnosti o brojevima
u ovisnosti o brojevima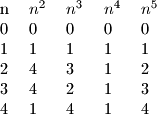
Primjetimo da su stupci
 i
i 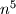 potpuno isti. Dakle znamo da uvjek vrijedi
potpuno isti. Dakle znamo da uvjek vrijedi 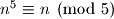 to jest
to jest 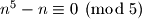
Potrebno je dakle jos provjeriti za koje
 vrijedi
vrijedi 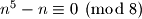
Promatrajmo ostatke koje pete potencije daju pri djelnjenju s
 u ovisnosti o brojevima
u ovisnosti o brojevima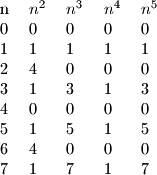
Dakle,
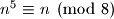 ako i samo ako je
ako i samo ako je 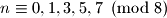 . Dakle,
. Dakle, 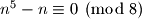 vrijedi za sve
vrijedi za sve  koji su djeljivi s
koji su djeljivi s  ili su neparni.
ili su neparni.  Školjka
Školjka 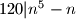 ?
?