Točno
13. studenoga 2013. 20:28 (12 godine, 4 mjeseci)
Sakrij rješenje
Odredi najmanji prirodni broj

tako da je polovina od

kvadrat nekog prirodnog broja, trećina od

kub nekog prirodnog broja, a petina od

peta potencija nekog prirodnog broja.
%V0
Odredi najmanji prirodni broj $n$ tako da je polovina od $n$ kvadrat nekog prirodnog broja, trećina od $n$ kub nekog prirodnog broja, a petina od $n$ peta potencija nekog prirodnog broja.
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
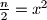
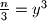
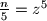
Znamo da je

djeljiv s

,

i

. Kako trazimo najmanji

, mozemo uzeti da nije djeljiv niti sa jednim drugim prostim brojem.
Tada je

oblika
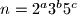
. Ako je
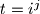
, onda su svi eksponenti protih brojeva u raspisu broja

djeljivi s

.
Iz
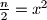
dobivamo
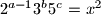
pa su

,

i

parni.
Iz
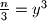
dobivamo
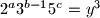
pa su

,

i

djeljivi s

.
Iz
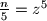
dobivamo
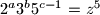
pa su

,

i

djeljivi s

.

je najmanji broj takav da je

paran i

i

djele

. Lagano se vidi da je to


je najmanji broj takav da je

djeljiv s

i

i

djele

. Lagano se vidi da je to


je najmanji broj takav da je

djeljiv s

i

i

djele

. Lagano se vidi da je to

Dakle,
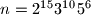
%V0
$\frac{n}{2}=x^2$
$\frac{n}{3}=y^3$
$\frac{n}{5}=z^5$
Znamo da je $n$ djeljiv s $2$, $3$ i $5$. Kako trazimo najmanji $n$, mozemo uzeti da nije djeljiv niti sa jednim drugim prostim brojem.
Tada je $n$ oblika $n=2^a3^b5^c$. Ako je $t=i^j$, onda su svi eksponenti protih brojeva u raspisu broja $t$ djeljivi s $j$.
Iz $\frac{n}{2}=x^2$ dobivamo $2^{a-1}3^b5^c=x^2$ pa su $a-1$,$b$ i $c$ parni.
Iz $\frac{n}{3}=y^3$ dobivamo $2^{a}3^{b-1}5^c=y^3$ pa su $a$,$b-1$ i $c$ djeljivi s $3$.
Iz $\frac{n}{5}=z^5$ dobivamo $2^{a}3^b5^{c-1}=z^5$ pa su $a$,$b$ i $c-1$ djeljivi s $5$.
$a$ je najmanji broj takav da je $a-1$ paran i $3$ i $5$ djele $a$. Lagano se vidi da je to $15$
$b$ je najmanji broj takav da je $b-1$ djeljiv s $3$ i $2$ i $5$ djele $b$. Lagano se vidi da je to $10$
$c$ je najmanji broj takav da je $c-1$ djeljiv s $5$ i $3$ i $2$ djele $c$. Lagano se vidi da je to $6$
Dakle, $n=2^{15}3^{10}5^{6}$
| 16. studenoga 2013. 22:32 | grga | Točno |
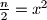
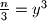
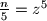
 djeljiv s
djeljiv s  ,
,  i
i  . Kako trazimo najmanji
. Kako trazimo najmanji  , mozemo uzeti da nije djeljiv niti sa jednim drugim prostim brojem.
, mozemo uzeti da nije djeljiv niti sa jednim drugim prostim brojem. oblika
oblika 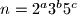 . Ako je
. Ako je 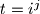 , onda su svi eksponenti protih brojeva u raspisu broja
, onda su svi eksponenti protih brojeva u raspisu broja  djeljivi s
djeljivi s  .
.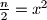 dobivamo
dobivamo 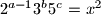 pa su
pa su  ,
, i
i  parni.
parni.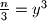 dobivamo
dobivamo 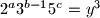 pa su
pa su  ,
, i
i  djeljivi s
djeljivi s  .
.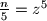 dobivamo
dobivamo 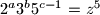 pa su
pa su  ,
, i
i  djeljivi s
djeljivi s  .
. je najmanji broj takav da je
je najmanji broj takav da je  paran i
paran i  i
i  djele
djele  . Lagano se vidi da je to
. Lagano se vidi da je to 
 je najmanji broj takav da je
je najmanji broj takav da je  djeljiv s
djeljiv s  i
i  i
i  djele
djele  . Lagano se vidi da je to
. Lagano se vidi da je to 
 je najmanji broj takav da je
je najmanji broj takav da je  djeljiv s
djeljiv s  i
i  i
i  djele
djele  . Lagano se vidi da je to
. Lagano se vidi da je to 
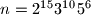
 Školjka
Školjka