Točno
13. studenoga 2013. 20:34 (11 godine, 3 mjeseci)
Dokaži da ako su brojevi
i
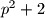
prosti, onda je i
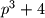
prost.
%V0
Dokaži da ako su brojevi $p$ i $p^2+2$ prosti, onda je i $p^3 +4$ prost.
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
Kako se spominje kvadrat, ponovno cemo gledati ostatke pri djeljenju s
.
Pogledajmo koje ostatke kvadrati daju pri djeljenju s
:
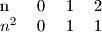
Dakle, ako
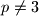
onda je
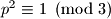
pa je
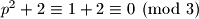
pa ocito nije prost.
Dakle,
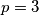
pa je
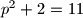
, a
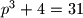
sto je prost broj.
%V0
Kako se spominje kvadrat, ponovno cemo gledati ostatke pri djeljenju s $3$.
Pogledajmo koje ostatke kvadrati daju pri djeljenju s $3$:
$$$\begin {tabular}{l l l l}
n&0&1&2\\
$n^2$&0&1&1
\end {tabular}$$$
Dakle, ako $p \neq 3$ onda je $p^2 \equiv 1 \pmod 3$ pa je $p^2 + 2 \equiv 1 + 2 \equiv 0 \pmod 3$ pa ocito nije prost.
Dakle, $p=3$ pa je $p^2+2=11$, a $p^3+4=31$ sto je prost broj.
| 16. studenoga 2013. 22:37 | grga | Točno |
Školjka