Kliknite ovdje kako biste prikazali rješenje.
Promotrimo najprije ploču 8x8 prije uklanjanja kutnih polja. Takvu ploču možemo popuniti sa 16 zadanih oblika. Zatim, obojimo svako polje koje "strši" u zadanim oblicima L, tj. ona polja koja su samo jednom stranicom povezana s ostalim poljima svog oblika. Takvim ćemo postupkom obojiti u svakom obliku po jednu pločicu. Dakle, svaka pločica prekrivat će jedno obojeno polje i tri neobojena polja. Na ploči će tada biti ukupno 16 obojenih i 48 neobojenih polja.
Primijetimo da će se dvije obojene pločice naći u kutnim poljima. Sada uklonimo kutna polja. Time smo uklonili ukupno 4 polja, dva obojena i dva neobojena. Dakle, broj preostalih obojenih polja je 14, a neobojenih 46. Dobiveni oblik treba prektiti s 15 zadanih pločica. Na takvih 15 pločica imamo 15 obojenih i 45 neobojenih polja (ranije smo konstatirali da na jednoj pločici imamo 1 obojeno i 3 neobojena). Dobili smo kontradikciju, odnosno, nedostaje nam jedno obojeno polje, a imamo jedno neobojeno polje viška.
Zaključno, nije moguće popuniti ploču 8x8 bez kutnih bolja zadanim oblicima.
 Školjka
Školjka 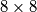 bez kutnih polja prekriti s
bez kutnih polja prekriti s  pločica oblika
pločica oblika  ili
ili  ?
?