Točno
15. studenoga 2013. 15:02 (12 godine, 2 mjeseci)
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
Kliknite ovdje kako biste prikazali rješenje.
Neka je napisano n brojeva.
Primijetimo da je maksimalni broj u nizu invarijantan, neka je to broj m. Tada je suma svih brojeva najvise nm. Ako primijenimo prvu transformaciju, suma svih brojeva se povecava. Nakon druge transformacije suma se sigurno ne smanjuje, a ne povecava se samo kada je x - 1 = y. U tom se slucaju radi o zamjeni dvaju uzastopnih brojeva u nizu pa se ukupan broj inverzija u nizu smanjuje (brojevi a i b cine inverziju ako i samo ako je a > b i a se nalazi prije b u nizu).
Pretpostavimo sada suprotno tvrdnji zadatka. Buduci da se suma svih brojeva ne smanjuje i pritom je ogradjena odozgo, broj iteracija u kojima se ona povecava mora biti konacan. To znaci da ona ostaje ista u beskonacno mnogo iteracija, odnosno da se broj inverzija smanjuje u beskonacno mnogo iteracija, sto nije moguce jer je nenegativan. Zakljucujemo da je moguce napraviti samo konacan broj iteracija.
Primijetimo da je maksimalni broj u nizu invarijantan, neka je to broj m. Tada je suma svih brojeva najvise nm. Ako primijenimo prvu transformaciju, suma svih brojeva se povecava. Nakon druge transformacije suma se sigurno ne smanjuje, a ne povecava se samo kada je x - 1 = y. U tom se slucaju radi o zamjeni dvaju uzastopnih brojeva u nizu pa se ukupan broj inverzija u nizu smanjuje (brojevi a i b cine inverziju ako i samo ako je a > b i a se nalazi prije b u nizu).
Pretpostavimo sada suprotno tvrdnji zadatka. Buduci da se suma svih brojeva ne smanjuje i pritom je ogradjena odozgo, broj iteracija u kojima se ona povecava mora biti konacan. To znaci da ona ostaje ista u beskonacno mnogo iteracija, odnosno da se broj inverzija smanjuje u beskonacno mnogo iteracija, sto nije moguce jer je nenegativan. Zakljucujemo da je moguce napraviti samo konacan broj iteracija.
 Školjka
Školjka  and
and  such that
such that 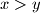 and
and  by either
by either 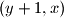 or
or 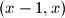 . Prove that she can perform only finitely many such iterations.
. Prove that she can perform only finitely many such iterations.