Neocijenjeno
15. travnja 2025. 00:12 (10 mjeseci, 1 tjedan)
Let
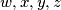
are non-negative reals such that
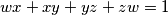
. Show that
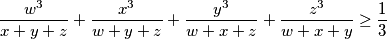
.
%V0
Let $w, x, y, z$ are non-negative reals such that $wx + xy + yz + zw = 1$. Show that
$$\frac {w^3}{x + y + z} + \frac {x^3}{w + y + z} + \frac {y^3}{w + x + z} + \frac {z^3}{w + x + y}\geq \frac {1}{3}$$.
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
Iz uvjeta imamo
$$(x+z)(w+y)=1\implies x+y+z+w\stackrel{\text{AG}}{\ge}2\sqrt{(x+z)(w+y)}=2$$
Nadalje, koristeći nejednakost između potencijskih sredina imamo
$$x^{\frac{3}{2}}+y^{\frac{3}{2}}+z^{\frac{3}{2}}+w^{\frac{3}{2}}\ge \frac{(x+y+z+w)^{\frac{3}{2}}}{2}$$
Konačno, $CSB$ u Engel formi nam daje
$$\frac {w^3}{x + y + z} + \frac {x^3}{w + y + z} + \frac {y^3}{w + x + z} + \frac {z^3}{w + x + y}\ge\frac{(x^{\frac{3}{2}}+y^{\frac{3}{2}}+z^{\frac{3}{2}}+w^{\frac{3}{2}})^2}{3(x+y+z+w)}\ge \frac{\frac{(x+y+z+w)^3}{4}}{3(x+y+z+w)}\ge \frac{(x+y+z)^2}{12}\ge \frac{1}{3}$$