Školjka

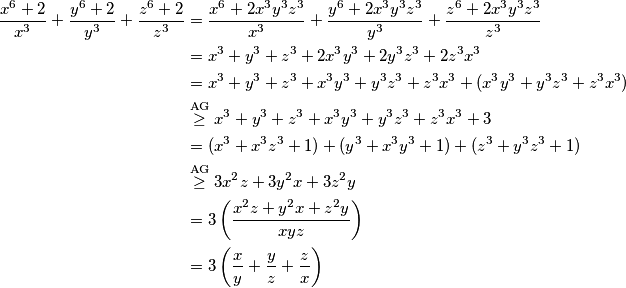
Koristeći uvjet zadatka imamo \begin{align*} \frac{x^6 + 2}{x^3} + \frac{y^6 + 2}{y^3} + \frac{z^6 + 2}{z^3}&=\frac{x^6 + 2x^3y^3z^3}{x^3} + \frac{y^6 + 2x^3y^3z^3}{y^3} + \frac{z^6 + 2x^3y^3z^3}{z^3}\\ &=x^3+y^3+z^3+2x^3y^3+2y^3z^3+2z^3x^3\\ &=x^3+y^3+z^3+x^3y^3+y^3z^3+z^3x^3+(x^3y^3+y^3z^3+z^3x^3)\\ &\stackrel{\text{AG}}{\ge}x^3+y^3+z^3+x^3y^3+y^3z^3+z^3x^3+3\\ &=(x^3+x^3z^3+1)+(y^3+x^3y^3+1)+(z^3+y^3z^3+1)\\ &\stackrel{\text{AG}}{\ge} 3x^2z+3y^2x+3z^2y\\ &=3\left(\frac{x^2z+y^2x+z^2y}{xyz}\right)\\ &=3\left( \frac{x}{y} + \frac{y}{z} + \frac{z}{x} \right) \end{align*}