Školjka

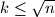
%V0 $\displaystyle p^{\lfloor log_p \sqrt{n} \rfloor} | n$ $\displaystyle \prod{p_i^{\lfloor log_{p_i} \sqrt{n} \rfloor}} | n$ $ \lfloor a \rfloor > a - 1$ $\displaystyle n \geqslant \prod{{p_i}^{\lfloor log_{p_i} \sqrt{n} \rfloor}} > \prod{\frac{\sqrt{n}}{p_i}}$ Promatrajmo samo proste brojeve 2,3,5,7 i 11 $\displaystyle n > \frac{n^{\frac{5}{2}}}{2 * 3 * 5*7*11}$ $2*3*5*7*11 > n^{\frac{3}{2}} $ $14 > \sqrt{n}$ Eliminacijom zaključujem $\sqrt{n} = 4$, to jest, $n=24$