Točno
2. prosinca 2013. 02:22 (10 godine, 5 mjeseci)
Dokaži da za sve
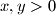
vrijedi nejednakost
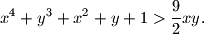
%V0
Dokaži da za sve $x,y>0$ vrijedi nejednakost $$
x^4+y^3+x^2+y+1>\dfrac 92 xy.
$$
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
%V0
$(x^4+x^2+1) + (y^3+y) \geqslant 3x^2 + 2y^2 \geqslant 2 \sqrt{6x^2y^2} = xy \cdot 2 \sqrt{6} > \frac{9}{2}xy $
Školjka 