Točno
2. prosinca 2013. 02:29 (10 godine, 5 mjeseci)
Neka je
realan broj,
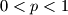
, a
prirodan broj. Dokaži da vrijedi nejednakost
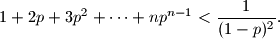
%V0
Neka je $p$ realan broj, $0<p<1$, a $n$ prirodan broj. Dokaži da vrijedi nejednakost $$
1+2p+3p^2+\dots+np^{n-1}<\dfrac1{(1-p)^2}.
$$
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
%V0
$\displaystyle \frac{1}{1-p} = \sum\limits_{i=0}^{\infty}{p^i}$
$RHS = \displaystyle \frac{1}{(1-p)^2} = \sum\limits_{i=0}^{\infty}{(i+1)p^i} > \sum\limits_{i=0}^{n-1}{(i+1)p^i} = LHS$
| 2. prosinca 2013. 08:55 | ikicic | Točno |
Školjka 
