Točno
3. prosinca 2013. 00:18 (11 godine, 2 mjeseci)
Nađite sva rješenja
jednadžbe:
(
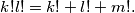
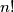
označava umnožak prirodnih brojeva od
do
.)
%V0
Nađite sva rješenja $k, l, m \in \mathbb{N}$ jednadžbe:
$$k!l! = k! + l! + m!\text{.}$$
($n!$ označava umnožak prirodnih brojeva od $1$ do $n$.)
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
%V0
Pretpostavimo $k,l \geqslant 4$
$m! = k!l! - k! - l! = (k!-1)(l!-1) -1 \geqslant 23k! - 24 \geqslant 22k!$
$ \Rightarrow m \geqslant k, l$
$k! | k! + l! + m!$
$k| l!$
Analogno mozemo zakljuciti $l! | k!$
$\Rightarrow k=l$
$k!^2 = 2k! + m!$
$m! = k! (k! - 2)$
$2 || k! - 2 \Rightarrow m \leqslant k + 3$ (zakljuceno iz $v_2(LHS)=v_2(RHS)$)
Provjerom ($m=k$, $m=k+1$...) zakljucujemo da jednadzba nema rjesenja za $k,l\geqslant 4$
Provjerom za $k \leqslant 3$ zakljucujemo da je jedino rjesenje $(3,3,4)$
| 3. prosinca 2013. 17:08 | ikicic | Točno |
Školjka 
(zakljuceno iz 
)
, 
...) zakljucujemo da jednadzba nema rjesenja za 
zakljucujemo da je jedino rjesenje 