Točno
3. prosinca 2013. 21:32 (12 godine, 3 mjeseci)
Dana je ploča dimenzija
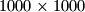
. Je li moguće obojati točno
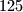
polja te ploče tako da svako od obojanih polja ima neparan broj obojanih susjeda?
Dva polja nazivamo
susjedima ako imaju zajedničku stranicu.
%V0
Dana je ploča dimenzija $1000\times 1000$. Je li moguće obojati točno $125$ polja te ploče tako da svako od obojanih polja ima neparan broj obojanih susjeda?
Dva polja nazivamo [i]susjedima[/i] ako imaju zajedničku stranicu.
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
Neka na svakoj plocici pise koliko ima susjeda.
Neka je

suma svih brojeva na plocicama.
Ako nema plocica,
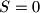
Ako dodamo plocicu, ona ima

susjeda, a

se poveca za
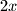
jer se svaki susjed poveca za

.
Dakle,
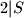
, iz cega zakljucujem da nije moguce.
%V0
Neka na svakoj plocici pise koliko ima susjeda.
Neka je $S$ suma svih brojeva na plocicama.
Ako nema plocica, $S=0$
Ako dodamo plocicu, ona ima $x$ susjeda, a $S$ se poveca za $2x$ jer se svaki susjed poveca za $1$.
Dakle, $2|S$, iz cega zakljucujem da nije moguce.
| 31. kolovoza 2015. 13:50 | grga | Točno |